Как не завалить ЕГЭ по математике. Чек-лист для экзамена

Известно, какие ошибки чаще всего допускают на ЕГЭ по математике. Репетитор Людмила Хорунжая разбирает каждую из них и рассказывает, чему надо обязательно научиться, чтобы не завалить ЕГЭ из-за банальной невнимательности.

В документе ФИПИ «Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2017 года по математике» приводится анализ типичных ошибок выпускников. И знаете, какая самая частая ошибка в первых двенадцати заданиях (базового и повышенного уровня)? Невнимательное чтение условия.

Школьники не видят в условии, что дано, как связаны между собой данные и, главное, что найти, на какой вопрос дать ответ. В таком случае уже становится неважно, что знает выпускник, как умеет применять знания для решения задачи. Он просто решает не ту задачу. Как если вы попросите купить молока, а принесут редис. И это в принципе иная ошибка, это не купить молоко с истекшим сроком годности.

Ошибка невнимательного чтения условия типична как минимум для семи заданий из двенадцати. Корни этой ошибки кроются в слабости навыка ориентировки в ситуации — хаотичности и отсутствии чёткого алгоритма рассмотрения задания.

Как разобраться в задании, чтобы ничего не перепутать

• прочитать задание;
• выписать, что дано (+сделать рисунок в геометрическом задании);
• установить и сформулировать письменно отношения и взаимосвязи между известными величинами;
• выписать, что найти, на какой вопрос дать ответ;
• определить, к какому типу относится задание;
• сформулировать содержание и последовательность действий при решении задания.

И уже после прохождения всех пунктов чек-листа приступать к решению. Важно именно выписывать, а не отмечать мысленно данные и условие — фиксировать их в материализованном виде. Очень уж часто решение в уме, без выписывания данных, пусть и краткого, но отображения хода решения, приводит к ошибкам невнимательности.

Вместо предварительной ориентировки в задаче, выяснении её условия, сути, требований и ожидаемого результата, школьники (и взрослые тоже) не медля после предъявления задачи, приступают к её решению. Вместе с тем, «свобода человека локализована в паузе между стимулом и реакцией» и именно в течение этой паузы можно сориентироваться в условии задачи, обдумать и спланировать её решение, или же понять, что задача субъективно сложная и лучше отложить её решение. Кроме сложности задания стоит учитывать и его трудоёмкость: как много времени займёт решение, как сильно я устану после этой задачи, хватит ли мне сил на другие задачи после решения этой или я уже не захочу их видеть.

Читайте также

4 способа подготовиться к ЕГЭ и не умереть от скуки

Ежедневно навык ориентировки проявляется (и формируется) в ответах на вопросы, которые мы сознательно задаём себе в новой ситуации: кто я, где я, что происходит, что требует ситуация, что я хочу, что я могу, как я поступлю? Такие вопросы помогают определить ситуацию, структурировать её, увидеть возможности и требования ситуации и действовать согласно им и своим целям.

Математические ошибки

Следующая по частоте типичная ошибка выпускников связана непосредственно с математическими знаниями. Так, ошибки в профильной математике в прошлом году вызваны неуверенным владением действиями со степенями, непониманием процентов, неумением определить знак тригонометрической функции, непониманием алгоритма исследования функций с помощью производной.

Интересно, как выпускники справляются с заданиями, когда понимают, что не могут довести решение до конца. Они предполагают хороший ответ (например, 1 или 2) и дают его без обоснования. Ответы в заданиях первой части действительно «хорошие» — целое число или конечная десятичная дробь. Так, ответ 0, (3) или иррациональное число указывает на неверное решение и необходимость проверки. В первых 12-ти заданиях обоснование решения не требуется и стратегия «хорошего ответа» даёт правильный ответ с вероятностью до 50%.

Вот, например, задания с «хорошим» ответом с точностью до знака. Старшеклассники быстро замечают, что в таких заданиях в ответе будет числовой множитель перед тригонометрическими функциями.

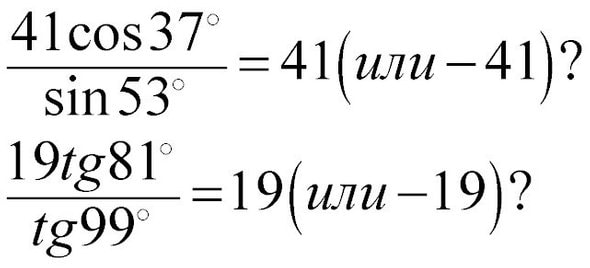
Несформированность пространственных представлений

Ещё один тип ошибок, которые встречаются в работах выпускников по профильной математике, связан с несформированностью пространственных представлений. К таким ошибкам в заданиях по геометрии относятся непонимание математической записи угла (<ABC≠<ACB), неверное чтение чертежа, незнание соотношений между величинами пространственных фигур (линейными размерами и площадью поверхности или объёмом). Кроме того, пространственные представления необходимы для понимания условия практико-ориентированных заданий и текстовых задач. Ошибки при нахождении скорости движения по течению или против течения реки, при нахождении величины скидки или стоимости товара до скидки, при определении массы вещества в растворе или сплаве также вызваны несформированностью пространственных представлений. Ситуация, когда школьник не понимает условие задачи, не понимает сам текст задачи, также относится к слабости пространственных представлений.

Сформированность пространственных представлений означает умение определить соотношения между объектами или явлениями и их характеристиками, умение определить временную последовательность событий.

Незрелость пространственных функций проявляется:

• в трудностях ориентации по карте;
• в сложностях различения право/лево;
• в устойчивых трудностях понимания условия задач (те самые логико-грамматические конструкции);
• в зеркальном написании цифр и букв;
• в зеркальном чтении примеров (вместо 42-8= читает 24-8=);
• в трудностях усвоения разряда числа (единицы, десятки, сотни…. Или десятые, сотые, тысячные…);
• в трудностях устного счёта с переходом через десяток (91-27=);
• в трудностях ориентировки на листе бумаги (отступы, порядок и структура в записи решения задачи, «скачущие» буквы и строки).

С точки зрения нейропсихологии «пространственные» ошибки выпускников обусловлены как непосредственно слабостью пространственных представлений, так и несформированностью и неустойчивостью зрительных представлений геометрических фигур (узнавание геометрических фигур и понимание их свойств).

Пример задачи, решение которой требует пространственных представлений как непосредственно в геометрии, так и для понимания условия.

Типичные ошибки участников ЕГЭ по профильной математике в заданиях с кратким ответом вызваны невнимательным чтением условия, слабостью собственно математических знаний и несформированностью пространственных представлений.

Для выпускников, планирующих сдать экзамен на 80± баллов, уверенное и безошибочное выполнение первых 12-ти заданий — необходимая основа для выполнения заданий части С. Кроме того, ошибки в этих заданиях особенно обидны — на них теряеются «лёгкие» баллы, те же баллы на заданиях части С получить гораздо сложнее. Для выпускников, планирующих сдать экзамен на 50-60 тестовых баллов (и решающих преимущественно только первую часть), ошибки в первых 12-ти заданиях существенно влияют на результат — каждый первичный балл стоит от 4 до 6 тестовых. Выпускникам, которым профильная математика нужна для галочки и «лишь бы сдать», ошибки (и особенно ошибки невнимательности) могут существенно испортить планы.

Читайте также

Все жалуются, что детей натаскивают на ЕГЭ. А может, это и неплохо?

Знание типовых ошибок и своих «любимых» ошибок можно продуктивно использовать на экзамене. Во-первых, ошибаются все, и это нормально. Важно признавать за собой право на ошибку по какой угодно причине и особенно в ситуации экзамена, заранее иметь в виду «я мог или могла ошибиться». И во-вторых, с учётом этого предположения проверять и перепроверять ещё дважды свои решения, ответы к заданиям, заполненные бланки ответов. Навык самопроверки — важная часть уверенности в себе, в своих силах, в своих решениях: я понимаю ход своих мыслей, могу воспроизвести решение и проверить себя, сначала я самостоятельно проверяю и оцениваю себя, лишь потом кто-то внешний. И конечно, навыку самопроверки тоже нужно учиться.

Фото: Unsplash (wu yi)