Заместитель председателя региональной предметной комиссии по математике ГИА-11 в Москве, ведущий специалист Московского центра качества образования Марина Черняева рассказывает, на что обратить внимание при подготовке к ЕГЭ по математике профильного уровня и что важно знать для решения заданий высокого уровня сложности.
Как устроен экзамен
Экзаменационная работа по математике профильного уровня сложности состоит из двух частей: первая часть — 12 заданий, в которых надо указать только ответ: семь из них базового уровня сложности (№ 1–4, 6–8) и пять заданий повышенного уровня сложности (№ 5, 9–12). Ответ в каждой из 12 задач — это либо конечная десятичная дробь, либо целое число. Каждое верно решенное задание оценивается одним баллом. Проверяется первая часть ЕГЭ профильного уровня с использованием специальных аппаратно-программных средств. Максимальный балл за нее — 12 первичных баллов.
В первой части экзаменационной работы появилось еще одно задание по планиметрии базового уровня сложности по теме «Векторы». Остальное осталось без изменений.
Задания первой части сгруппированы по темам. Сначала три задания по геометрии: два из них по планиметрии (причем задание № 1 может касаться рассмотрения треугольников и их свойств, четырехугольников и их свойств, окружности и ее элементов, вписанных и описанных окружностей, а вот задание № 2 будет только на тему «Векторы» на плоскости) и задание № 3 по стереометрии. Затем два задания по теории вероятностей и статистике (№ 4 — базового уровня сложности, № 5 — повышенного уровня), далее следует блок заданий по алгебре и началам математического анализа.
Вторая часть экзамена состоит из семи заданий с развернутым ответом. Это значит, что надо записать обоснованное решение, которое приводит к ответу. Пять заданий второй части — задания повышенного уровня: три по алгебре (№ 13, 15, 16 — уравнение, неравенство, текстовая задача с экономическим содержанием) оцениваются в два балла (т. е. за их решение можно получить от ноля до двух баллов); два задания по геометрии (№ 14, 17 — стереометрическая и планиметрическая задачи) оцениваются в три балла (от ноля до трех баллов).
При решении обеих геометрических задач надо ответить на два вопроса: в пункте «а» доказать некоторое геометрическое утверждение, теоретически обосновав все шаги решения, а в пункте «б» вычислить требуемую геометрическую величину: угол, отрезок, площадь, объем. Все шаги решения пункта «б» также должны содержать обоснования: в первую очередь теоретическое подтверждение, что именно надо найти — данный угол или отрезок (если вы сначала строите угол (отрезок), то его построение также должно быть прописано и доказано), далее нужно теоретически обосновать выкладки и вычисления. Последние два задания второй части — задачи высокого уровня сложности № 18 и 19: исследование, связанное с параметром, и задача «на числа» соответственно. Они оцениваются максимально в четыре первичных балла.
Вторая часть экзаменационной работы проверяется на основе разработанной системы критериев оценивания
Контрольные измерительные материалы содержат и справочный материал, но в него входят четыре формулы по тригонометрии. Правда, выполнив определенные преобразования, из них можно получить достаточно важные формулы для решения уравнений и преобразования выражений (частный случай задания № 6, 7, 13, если в условии будет задано тригонометрическое выражение). Остальные формулы нужно запомнить. Чаще всего они несложны, но выводить их на экзамене нецелесообразно, так как может не хватить времени на выполнение всей работы. Желательно в процессе повторения эти формулы запоминать, сначала используя справочные материалы, а далее уже воспроизводить по памяти.
Таким образом, контрольные измерительные материалы ЕГЭ профильного уровня по математике содержат 19 заданий, время выполнения работы — 3 часа 55 минут (235 минут), максимальный первичный балл за всю работу — 32. Обратите внимание: есть минимальный порог для получения аттестата о среднем общем образовании, а есть минимальный порог для поступления в государственные вузы (он выше, чем порог для получения аттестата).
Что нового будет в 2024 году и как решать эти задания
В экзаменационной работе появилось новое геометрическое базовое конкретное задание по теме «Векторы». В последние годы задача, касающаяся векторов на первой (геометрической) позиции, не встречалась, хотя тема «Векторы» достаточно подробно изучается как в 9-х, так и в 11-х классах, и векторы имеют достаточно большое прикладное применение не только в физике, но и при решении задач по геометрии координатно-векторным способом.
Что надо уметь при работе с векторами?
- Определять векторы и уметь откладывать вектор от произвольной точки;
- Определять равные и противоположные векторы и уметь их откладывать от произвольной точки;
- Определять сонаправленные и противоположно направленные векторы, коллинеарные векторы, знать признак коллинеарности векторов;
- Строить вектор суммы векторов, вектор разности, вектор, который получается при умножении вектора на число, не равное нулю;
- Раскладывать вектор на плоскости по двум неколлинеарным векторам;
- Находить координаты вектора, координаты вектора суммы и разности, вектора, полученного в результате умножения вектора на число;
- Находить длину (модуль) вектора по его координатам.
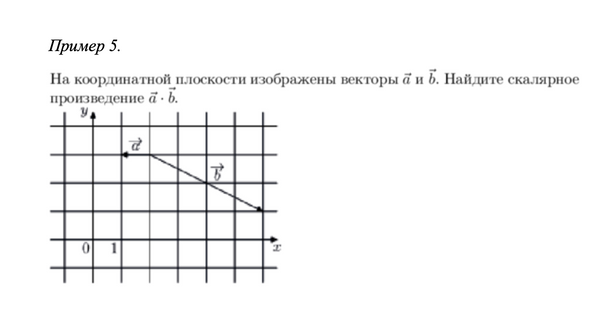
Также стоит обратить внимание на скалярное произведение двух ненулевых векторов, именно оно связывает координаты векторов с их длиной и углом между ними.
Повторяя целенаправленно эту тему, прорешайте задачи после каждого параграфа учебного пособия и дополнительные задачи по теме. Далее переходите к заданиям открытого банка ФИПИ. При возникновении вопросов проконсультируйтесь с учителем и посмотрите разбор решения заданий, стоящих на данной позиции.
Это задание базового уровня сложности, причем достаточно конкретное (оно касается только векторов на плоскости), поэтому надо постараться отработать все возможные задачи, чтобы свободно и быстро справиться с ним на экзамене.
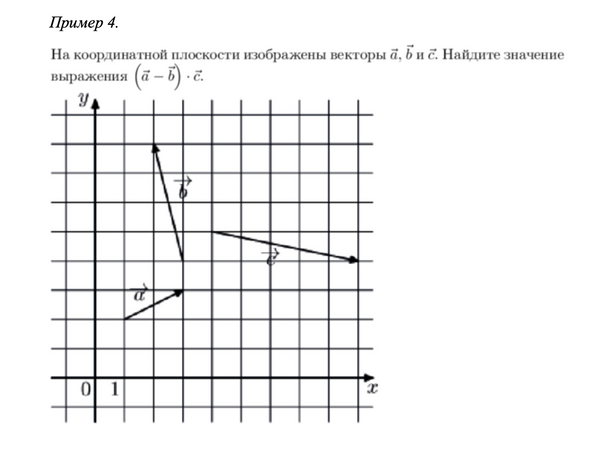
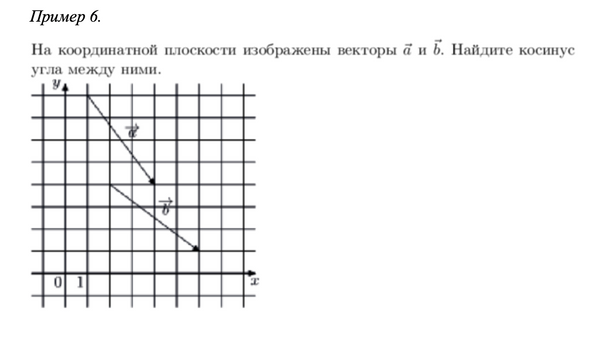
Примеры возможных заданий на данной позиции
Если вы хорошо разобрали все вопросы, связанные с векторами на плоскости, изучите материал по этой теме в разделе «Стереометрия». Возможно, это позволит вам решить пункт «а» или «б» в задании на 14-й позиции, а также в задании повышенного уровня сложности по стереометрии. Наиболее подходящими конструкциями для использования координатно-векторного метода решения являются куб, прямоугольный параллелепипед, правильная треугольная, четырехугольная, шестиугольная призма и пирамида, прямая призма или пирамида с ромбом в основании. Именно эти тела наиболее просто расположить в прямоугольной системе координат с заданными базисными векторами.
Если нужно найти длину отрезка, то можно найти длину вектора, равного по длине данному отрезку. Но для этого нужно найти его координаты и использовать далее скалярное произведение.
Если надо найти угол между прямыми, то сначала нужно найти модуль косинуса угла между векторами, лежащими на данных прямых, затем уже сам угол. Для этого предварительно надо найти координаты обоих векторов и применить далее скалярное произведение векторов. Обратите внимание на разницу угла между векторами и угла между прямыми, на которых они лежат. Угол между пересекающимися прямыми, если они не перпендикулярны, это всегда меньший угол с вершиной в точке пересечения (острый), и прямой, если прямые перпендикулярны. А вот угол между векторами — это тот угол, который образует их «направления» (пробегает все значения от ноля до 180 градусов).
Если надо найти угол между прямой и плоскостью, то работаем с вектором, лежащим на прямой, и направляющим вектором плоскости. Здесь понадобится уравнение плоскости, а следовательно, координаты точек, задающих плоскость. В этом случае необходимо найти координаты точек, являющихся вершинами (иногда не всех вершин), и точек, заданных в условии; записать уравнение плоскости и далее действовать в соответствии с вопросом задачи. В этой ситуации надо хорошо знать решение прямоугольных треугольников, значение тригонометрических функций стандартных углов. А еще знать уравнение плоскости, уметь решать систему трех линейных уравнений, обладать хорошими вычислительными навыками.
В процессе подготовки к решению стереометрической задачи на экзамене нужно решить координатно-векторным способом несколько задач и внимательно разобрать решение. А еще лучше попробовать решить одну и ту же задачу двумя способами, чтобы не тратить время на экзамене на выбор способа решения.
Обратите внимание, что появление нового, пусть и простого задания не увеличивает время, отведенное на выполнение работы, поэтому постарайтесь готовиться к экзамену интенсивно и качественно, чтобы сократить время на верное выполнение первой части и качественное решение заданий с развернутым ответом.
Как лучше готовиться к экзамену
Для успешной подготовки рекомендуем выпускникам ознакомиться на сайте ФИПИ с кодификатором, спецификацией и демоверсией КИМ ЕГЭ по математике, а также с критериями оценивания заданий с развернутым ответом, которые размещены в демоверсии. Дополнительную информацию по заданиям можно найти в открытом банке заданий ЕГЭ на сайте ФИПИ.
Полезно будет поработать с навигатором самостоятельной подготовки к ЕГЭ. Помогут выпускникам и учителям видеоматериалы о ЕГЭ, в том числе вебинары, посвященные особенностям ЕГЭ 2024 года. Их можно найти на сайте Московского центра качества образования, Регионального центра обработки информации, в группе Московского центра качества образования социальной сети «ВКонтакте» и на сервисе Rutube.
В подготовке к экзамену важна практика. Поэтому выпускники могут принять участие в независимых диагностиках в формате ЕГЭ на базе Центра независимой диагностики (ЦНД) Московского центра качества образования. Они не только проходят в соответствии с реальной процедурой ЕГЭ, но и по актуальным версиям КИМ ЕГЭ 2024 года. Участие в таких диагностиках позволит выпускникам почувствовать себя в условиях реального экзамена и оценить уровень своей подготовки. Записаться на независимые диагностики в формате ЕГЭ можно на сайте Московского центра качества образования в разделе «ЦНД».
Московским выпускникам предоставляется уникальная возможность принять участие в единых городских контрольных работах. По итогам работ ведущие эксперты предметных комиссий проводят вебинары с анализом результатов и подробным разбором выполнения каждого задания, а также разбором типичных ошибок, их можно посмотреть на сайте Регионального центра обработки информации.
И независимые диагностики на базе ЦНД, и единые городские контрольные работы позволяют будущим выпускникам проверить уровень своих знаний и понять, какие темы стоит повторить. Образовательные организации, в свою очередь, могут определить уровень подготовки учащихся и скорректировать образовательные траектории для каждого школьника.
Фото на обложке: Владимир Смирнов / ТАСС