Высшая алгебра как основа интеллекта

Делюсь опытом занятий с подростками по ознакомлению их с полями Галуа и с группами перестановок, с которых началась высшая алгебра и без которых не было бы искусственного интеллекта (ИИ). Математику можно применять только к числам, поэтому занятия начинаются со знакомства преобразования текста в цифры. Введение операций над числами, которых нет в школьной программе, происходит через шифрование текстов. По завершению занятий подростки глубже осваивают программирование и без затруднений постигают принципы формирования ИИ, так как теперь они знакомы с операциями внутри ЭВМ и получили опыт преобразования внешней среды в цифровые символы.

Я придаю занятиям с подростками по высшей алгебре особое значение, так как Россия не выдвинулась в мировые лидеры создателей искусственного интеллекта (ИИ). Важнейшей причиной отставания от лидеров, на мой взгляд, является образовавшийся в стране дефицит кадров алгебраистов. Высшая алгебра описывает те операции, которые совершаются внутри любой вычислительной техники, основанной на электронике.

Для понимания важности проведения занятий с подростками в самом начале даётся оценка перспектив развития ИИ и рассматриваются причины, которые препятствовали подготовке кадров профессионалов со знаниями высшей алгебры.

Люди обычно узнают лишь о тех ИИ, которые имеют массовое применение и не требуют специальной подготовки для их использования, а реально в каждой отрасли существуют сотни и даже тысячи специализированных ИИ. Именно они формируют оценки объёмов разработок и продаж ИИ. Только в Сбербанке используется свыше 2000 самообучающихся ИИ в различных бизнес-процессах.

Все отрасли мировой экономики показывают устойчивый рост спроса на ИИ.

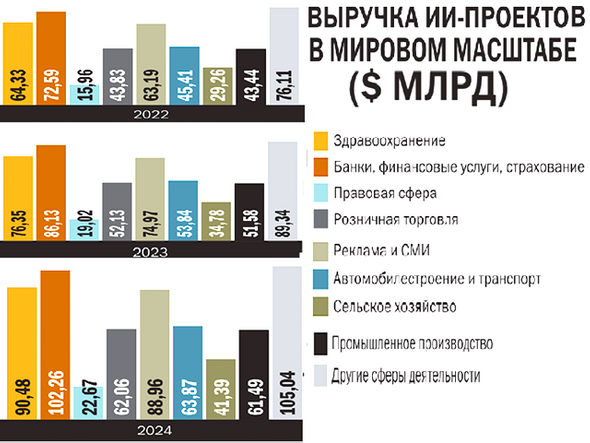
По итогам 2024 года объем отечественного рынка ИИ достиг всего лишь $1,45 млрд. По итогам за десять месяцев 2025 года совокупный трафик на ИИ-сервисы вырос почти в шесть раз, а лидером стал ChatGPT, завладев почти 40% в среде российских потребителей, на втором месте — Deepseek, на третьем — GigaChat. При этом совокупная доля трафика на российские решения GigaChat и «Алису AI» составила 13%. Как видим, даже на отечественном рынке российские разработчики ИИ не смогли занять лидирующие позиции.

Почему же Россия не стала одним из лидеров по разработкам ИИ?

Я склонен считать, что такое произошло из-за состояния подготовки кадров по дискретной математике. Хотя мы все уверены, что Россия всегда была сильна своими математиками, но это верно для направлений классической математики, но не для дискретной. Классическая математика развивалась под задачи промышленного производства, а дискретная математика стала востребована для создания информационных технологий, к которым относится ИИ.

В нашей стране был период, когда отношение к специалистам в области дискретной математики было отрицательным. Вот цитаты из Литературной газеты от 5 апреля 1952 года: «Буржуазная печать широко разрекламировала новую науку — кибернетику. Эта модная лжетеория, выдвинутая группкой американских «учёных…» … «По утверждению кибернетиков, поводом к созданию их лженауки послужило сходство между мозгом человека и современными сложными машинами».

После таких статей далеко не каждый мог решиться на преподавание высшей алгебры, а именно она лежит в основе кибернетики. Итак, нет ничего удивительного, что почти никто ничего не знал о числах в двоичной системе счислений, а поля Галуа относили к той математике, которая доступна только вундеркиндам.

Для талантливой молодёжи создавались спецшколы и интернаты, где воспитывали математиков самого высокого уровня, но не в дискретной математике. Чтобы в этом убедиться достаточно взглянуть на список тех, кто получил премию Фалкерсона, самую престижную премию в области дискретной математики. В этом списке нет ни одного российского учёного.

В 60-е годы, когда кибернетика вошла в моду, началось осознание того, что в стране возник недостаток специалистов по высшей алгебре. Её преподавали в ряде университетов, но не в школе и не в институте с подготовкой кадров для промышленности. В основном знакомили только с теми областями математики, которые получили толчок к развитию в XIX веке. Научные достижения в области математики, которые входили в реальную деятельность в первой половине XX века, оказались за бортом массового образования.

В 60-е годы попытки ввести элементы высшей математики в школьную программу были инициированы А. И. Маркушевичем (заместитель министра просвещения РСФСР в 1958–1964 гг.) и А. Н. Колмогоровым (ученый с мировым именем, возглавил в 1964 году математическую секцию комиссии по определению содержания среднего образования, созданной при АН СССР и АПН СССР). Они докладывали руководству страны, что дискретная математика, получившая развитие в XX веке, является основой информационных систем, которые во всё большей степени будут влиять на развитие любых отраслей экономики.

Начиная с 60-х годов в программу среднего образования стали добавлять разделы современной математики, но без высшей алгебры. Отказ от введения основ высшей алгебры обосновывался невозможностью подготовки преподавательского состава для массовой школы.

К этому добавилось ещё и то, что руководство страны особое внимание обратило на защиту информации, а поэтому все разработки по шифрам были засекречены. Механические шифраторы заменялись электронными, а для их разработки были привлечены лучшие алгебраисты того времени. Они при поиске решений по защите информации вносили наиболее существенный вклад в развитие высшей алгебры, но на их научных работах ставился гриф секретности. Тем самым остальные алгебраисты не могли ознакомиться с достижениями тех, кто оказался на острие дискретной математики.

Хорошо, что в университетах сохранялись фанатики, которые совершенствовали свои учебные курсы по дискретной математике. Одним из таких энтузиастов был Узков Александр Илларионович. В 1971 году из печати за его авторством вышел учебник «Группы и теория Галуа. Учебное пособие по курсу алгебры». Но ему для публичного издания пришлось переработать то, что он преподавал для подготовки криптографов, заменив шифры иными примерами.

Другие алгебраисты, которые преподавали дискретную алгебру, не могли использовать примеры шифров на своих занятиях даже при отсутствии личных связей с секретными службами. Это происходило по той причине, что в стране были запрещены к продаже любые книги для знакомства с криптографией, включая даже тех авторов, чьи книги лежали на прилавках книжных магазинов во многих странах мира. Тем самым повторить в полном виде курс Узкова, используя понятия шифров, было бы слишком рискованно.

В 1992 году было принято решение вывести из-под грифа секретности подготовку криптографов и создать Институт криптографии, связи и информатики (ИКСИ), который сейчас является одним из ведущих вузов страны по подготовке алгебраистов. Тем самым была открыта дорога всем, желающим заняться криптографией.

В том же 1992 году была издана первая книга на русском языке по криптографии. Это были «Тайны тайнописи» Германа Фролова (криптограф, полиглот, закончил мехмат МГУ). В своей книге он опасался дать то, о чём узнал в годы своей практической деятельности, ограничившись лишь реальными примерами из истории криптографии, но даже их он почерпнул из печатных изданий, лежавших в книжных магазинах тех стран, где он бывал.

После образования ИКСИ и выхода книги Фролова я решился на апробацию занятий с подростками по полям Галуа и по группам перестановок с использованием простейших шифров. К самой же идее начать работу именно с подростками меня подтолкнул Александр Нечаев. В его личном архиве были краткие записи лекций Узкова, которые он посещал в самом начале 60-х годов (Нечаев Александр Александрович, российский алгебраист с мировой известностью, заслуженный деятель науки Российской Федерации, доктор физико-математических наук, профессор, действительный член Академии криптографии Российской Федерации, профессор Института криптографии, связи и информатики, профессор кафедры теоретической информатики механико-математического факультета МГУ им. М. В. Ломоносова). Нечаев был даже уверен, что высшая алгебра легче будет усваиваться подростками, чем студентами, если начать знакомство с полями Галуа с помощью шифрования переписки.

В 90-е годы студенты редко увлекались высшей алгеброй из-за того, что они не видели её реального применения. Отсутствие понятных примеров по полям Галуа, связанных с практикой, породило высокий уровень формализма в изложении полей Галуа. Я не один раз убеждался в этом после бесед со студентами, которые имели отличные оценки по высшей алгебре, но не были способны назвать ни одного практического применения полей Галуа.

Криптография дала осязаемые образы для понимания многих свойств полей Галуа. Всё дело в том, что люди знали только десятичную систему счислений и срослись с ней, а устоявшиеся привычки мешали освоению двоичной системы счислений. Как это ни парадоксально, но этому способствовали успехи по развитию программирования, благодаря которым работа на ЭВМ перестала требовать знаний о битовых операциях. Если в первые годы развития ЭВМ программировали в ячейках с двоичными записями, то потом перешли на машинные языки, когда ЭВМ самостоятельно осуществляет перевод десятичной записи в двоичные коды, потом все операции проводит в двоичной системе, а в конце полученный двоичный результат переводит на язык, понятный оператору. Потребитель вычислительной техники не задумывается, каким образом его задание было переведено в систему с использованием математических операций, а тем более о той математике, без которой не работает ни одна ЭВМ. Но для создателей ИИ эти знания необходимы.

ИИ является результатом работы многих научных достижений, а в центре их находятся нейоробиология и дискретная математика. С одной стороны, востребованы знания по нейробиологии, о которых Константин Анохин читал лекции разработчикам ИИ (Константин Владимирович Анохин — российский нейробиолог, доктор медицинских наук, профессор, академик РАН, директор Института перспективных исследований мозга), а с другой стороны, эффективность ИИ зависит лишь от специалистов по дискретной математике.

Для занятий с подростками важно, что в криптографии задействованы операции, которые не связаны с каким-либо счислением. Через шифры подростки знакомились с новыми операциями, которые их мозг легко усваивал. Подчеркну, что высшая алгебра предполагает расширение понятий операций, а электроника формирует операции, которых нет в десятичной системе счислений.

Известно, что в электронике наличие тока означает 1, а его отсутствие означает 0. С записью чисел появляется возможность производить математические операции. Шифры составлялись из нулей и единиц, а поэтому операции с ними были понятны подросткам, хотя и не были операциями в привычной десятичной системе счисления.

Нет ничего удивительного в том, что А. Узков ввёл в свой учебный курс именно шифры. Он участвовал в подготовке отечественных криптографов, а поэтому его курс был естественным для студентов. Так было и у меня. Бывшие школьники пришли на мои занятия с желанием изучать шифры, а за счёт этого математика лишь с двумя обозначениями 1 и 0 воспринималась нормально, а тогда и вводимые операции, которых нет в десятичной системе, усваивались легко и быстро.

Ниже я даю описание основных подходов для курса по основам высшей алгебры с использованием простейших двоичных шифров. Эти шифры позволят дать первоначальные представления по высшей алгебре. При этом для понимания курса по высшей алгебре не востребованы разделы той математики, которые преподают в старших классах школы. Заявляя в подзаголовке к статье, что мои занятия для подростков, я хотел подчеркнуть, что знания о логарифмах, о синусах, о пределах, об интегралах не требуются, но способны затруднить освоение новых типов операций. Подчеркну ещё раз, что операции в полях Галуа и в группах, которые даются подросткам, естественны для внутренней работы любой электроники, включая нейросети ИИ, но не отражены в школьном курсе по математике.

Шифры мне помогали продемонстрировать естественность математических операций в полях Галуа, а потом на их основе я мог перейти к обобщающим понятиям конечных полей и алгебраических групп. Если курс для студентов обычно начинается со строгих математических определений, то при работе с подростками они сначала усваивают работу в полях Галуа на примерах, а потом лишь получают формулировки определений, точных с точки зрения формальной математики.

Подростки шли на первое занятие не за знаниями по высшей алгебре, а жаждали узнать что-то о шифрах. Я же в ходе занятий знакомил их с полями Галуа и алгебраическими группами, так как надо было пояснять свойства шифров. И ни один подросток не покинул моих занятий! Все были увлечены и с удовольствием не только играли в шифровки, но и старались понять то, что имеет отношение сначала к полям Галуа, а потом и к алгебраическим группам.

Итак, мы начали, как я обещал подросткам, с шифров. С одним из видов ручного шифра нас познакомил Конан Дойл в рассказе «Пляшущие человечки».

А что будет, если знаки заменить числами?

С числами можно вводить в употребление математические действия. При этом математические операции не обязаны быть теми же, с которыми знакомили в школе.

Я ознакомил подростков с телеграфными кодами, начиная с азбуки Морзе, чтобы естественным образом перейти к двоичной записи чисел и к полям Галуа характеристики 2.

Для первого знакомства с шифрованием я выбрал Международный телеграфный код 2 (МТК-2), который наиболее часто использовался для телеграфных сообщений. Реальная телеграфная аппаратура в прошлом веке была рассчитана именно на этот код.

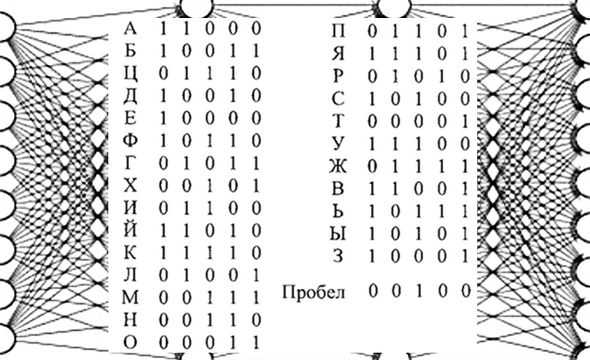
Короткое сообщение «БУДУ» в коде МТК-2 запишется так

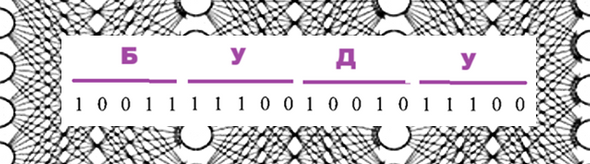
В шифровании будем применять операцию сложения по модулю 2.

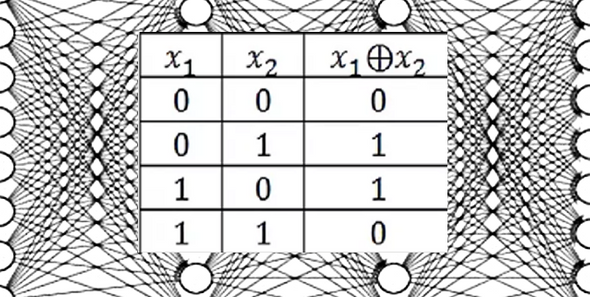
Вводим операцию сложения двух букв. Сложение букв в процессе шифрования производится по каждой отдельной двоичной (битовой) позиции.

Первую букву текста зашифровываем любой буквой, которая будет ключом шифра для данного текста. В этом примере взята буква Ф (10110), тем самым имеем Б+Ф=Х.

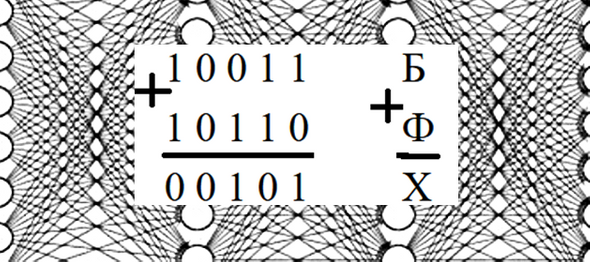
Вторая буква при шифровании складывается с первой буквой сообщения (У+Б=Ж), третья буквы складывается со второй буквой сообщения Д+У=Ц) и четвертая складывается с третьей (У+Д=Ц). Для текста любой длины простое правило: каждая буква сообщения складывается с предыдущей буквой из того же сообщения.

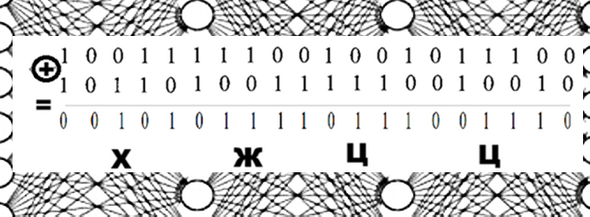
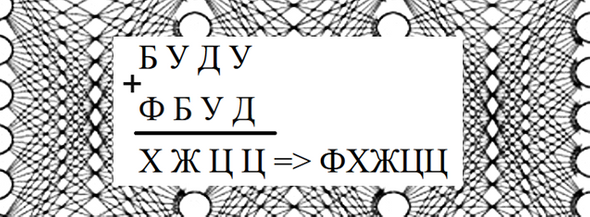
При отправке шифрованного текста необходимо указать получателю ещё и ключ, то есть ту букву, которой мы зашифровали первую букву текста, поэтому шифрованное сообщение примет следующий вид «ФХЖЦЦ».

Буква, сложенная сама с собой, даст строчку из пяти нулей 00000. Кроме неё могут появиться и другие строки, которые не отмечены у меня в таблице МТК-2. Для них мы с учениками придумывали дополнительные символы. Ведь зашифрованный текст будет содержать не 26 букв с 27-м пробелом, а все 32 строки с пятью битовыми позициями.

Если же возьмем за основу МТК-3, который с семью битами, то получим уже 128 булевых числа (два в степени 7). А если взять за основу не биты 0 и 1, а тройку 1, 2 и 3, то получаем всех строк, равное степени тройки. Если строка из двух ячеек, то строк будет 2 в степени 3, а если из четырёх ячеек, то 4 в степени 3. Здесь я знакомлю подростков с элементами комбинаторики, которая является ещё одной областью высшей математики.

У пляшущих человечков каждая буква заменяется на один и тот же символ. В рассказе Конан Дойля продемонстрировано, как это можно использовать для дешифровки. А вот в нашем случае при использовании только 0 и 1 метод вскрытия шифра должен быть другим. В нашем способе шифрования одна и та же буква текста получает несколько разных значений в шифрованном тексте. Ведь её значение в шифрованном тексте зависит от того, с какой буквой она была сложена, а эти буквы различны. Для вскрытия подобных шифров надо обладать знаниями о полях Галуа.

Теперь можно перейти к понятию изоморфизма. Сначала взглянем на определение поля Галуа в интернете или в учебнике. Мы там видим, что поле Галуа содержит q элементов, где q равно p в степени n => p — это максимальное число в ячейке (для нашего примера — 2), а n — это число ячеек в нашей строке (в примере — 5).

Когда мы шифровали текст кодом МТК-2, то получали два типа записей для операции сложения. Одна запись произведена в наших примерах через 5-разрядные строки с нулями и единицами, а другая запись оставляла буквы. Эти записи одного и того же поля Галуа, но на разных множествах: цифровом и буквенном. Обе записи одного и того же поля Галуа. Такие поля мы называем изоморфными. Это как бы меняются обозначения, а сами результаты операций при этом не меняются. Мы воспользовались той записью поля Галуа, с которой работает электроника.

На следующем этапе наших занятий вводим ещё один тип шифрования. Это — перестановки внутри строк каждой буквы. Запишем теперь шифрованный текст буквами по 5 бит друг под другом.

Колонки переставляем и получаем новый шифрованный текст. Для данного примера: колонка 1 переносится на место колонки 3, колонка 2 на место колонки 5, 3 на место 1, 4 на место 2, 5 на место 4.

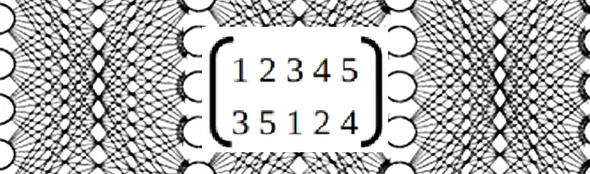
Из старого шифрованного текста ФХЖЦЦ получим новый УД+ВВ.

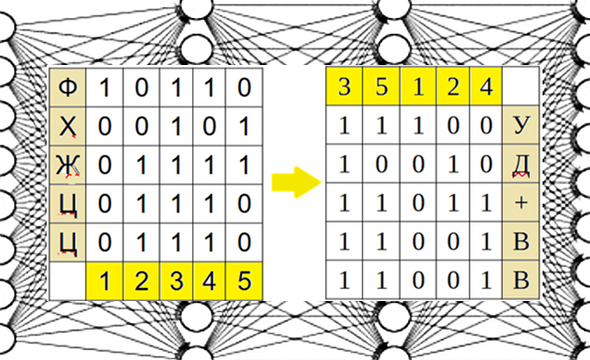
Для снятия шифрования применим ту перестановку, которая возвращает столбцы к первоначальному порядку.

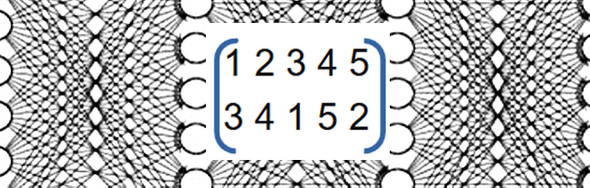
О перестановке шифровальщики договариваются заранее. После применения перестановки будут изменены все буквы первичного шифрованного текста, включая первую букву, которая была ключом для зашифровки первоначального текста. Теперь первичный ключ зашифрован, а поэтому не может быть известен постороннему, следовательно, никто не сможет использовать наш первичный ключ, чтобы расшифровать наш текст.

Понятно, что мы усложнили шифр, применив сначала сложение по модулю 2, а потом осуществив перестановку.

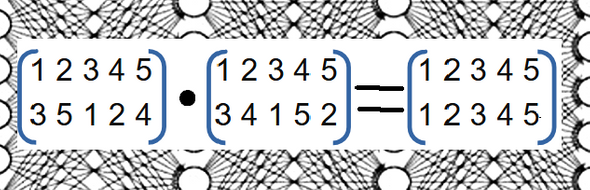
А как усложнится шифр, если применим одну перестановку, а потом за ней ещё одну перестановку? Для ответа на этот вопрос знакомимся с операцией умножения между перестановками.

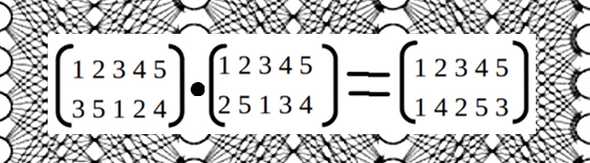
Убеждаемся, что шифр не усложняется, так как итог будет тот же, что и с одной перестановкой.

Подобную запись применения двух перестановок назвали умножением перестановок. Единичной перестановкой будет та, которая ничего не переставляет.

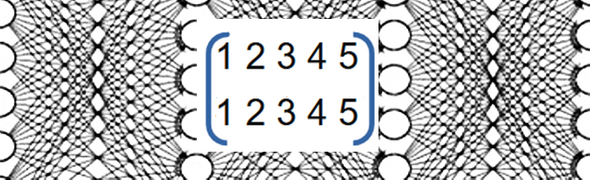
Определение единицы в группе перестановок естественно, так как умножение на 1 (единица) ничего не должно менять.

Ввели для операции умножения понятие единицы, а теперь можно вводить понятие обратной перестановки. Обратная, когда при умножении прямой и обратной перестановки получаем единицу.

На занятиях постоянно приходится задавать вопросы самим себе и тут же отвечать на них. К примеру, лучше переставить колонки в исходном тексте до их сложения (до первичного шифрования) или лучше переставить колонки после их сложении на первом этапе шифрования? Рассматриваем с подростками на примерах в ходе занятий.

Введение в тему перестановок позволяет перейти к алгебраическим группам. Она же будет той же самой группой автоморфизмов, которая была описана в работах Галуа.

Теперь подростки подготовлены для восприятия двоичного счисления и к сложению чисел в двоичной записи. Здесь реализован тот же принцип, что и сложение чисел в десятичной записи. Здесь осуществляется подобный же перенос в следующий разряд: 1+1=10 в двоичной системе счислений.

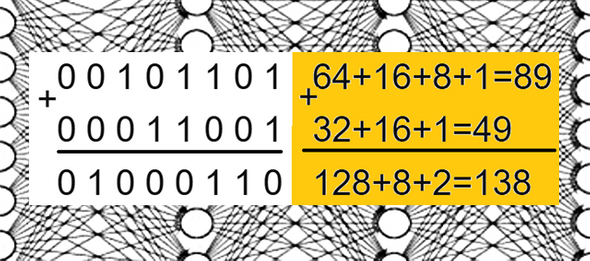
После освоения двоичной системы счислений переходим к переводу чисел из двоичной системы к десятичной и обратно. Складываем числа в двоичной системе и их же запись в десятичной системе. Убеждаемся, что результаты при переводе из одной системы в другую совпадают. Это и есть изоморфизм.

Отдельной темой показываем, что при решении задач в действительной области мы часто ограничиваемся определённым числом знаков после запятой. В таком случае мы можем переносить решение задач из действительного поля в конечное поле Галуа.

Теперь знакомим с главной теоремой Галуа про изоморфизм полей. Убеждаемся, что мы с помощью строк из 0 и 1 получаем все поля Галуа в булевой алгебре, а любые другие им изоморфны.

Обращаю особое внимание на то, что на занятиях подростки получили примеры того, что математик может выбирать число ячеек для проведения операций, а ещё он может выбирать даже сами операции. Это очень важно для понимания возможностей при разработках ИИ. В реальном мозгу, а теперь и в нейросети ИИ, при решении каждой задачи могут использоваться те или иные поля Галуа со своими группами автоморфизмов. Даже при решении одной задачи могут применяться несколько разных полей Галуа с разными операциями. Это подростки увидели в ходе двойного шифрования.

Теперь подростки вышли на тот этап занятий, когда затруднений с восприятием формальных математических определений и теорем не будет. В дальнейшем изоморфизм можно использовать, чтобы демонстрировать на занятиях не абстракции, а работать с той записью, которая удобна для иллюстрации в ходе подачи нового материал.

Итак, подростки уже подготовлены к восприятию основных теорем, На этом я завершаю знакомство с моими занятиями по высшей алгебре, а в интернете достаточно учебников, когда с их помощью каждый желающий способен сформировать свой индивидуальный курс по высшей алгебре для занятий с подростками.

Заключение

Итак, в ходе занятий мы заменяли буквы битами, проделывая с ними операции. После занятий подростки будут легко воспринимать переводы любых элементов в двоичную запись. Теперь не только буквы, а видимая картинка или услышанный звук легко переводятся в цифры. Создание ИИ начинается с перевода визуальной или слуховой картинки в биты, а теперь у подростка это не вызывает затруднений. Он может сравнивать разнообразные варианты этих преобразований, как сравнивал на занятиях азбуку Морзе и международные коды.

После перевода в цифры совсем не обязательно с ними проделывать операции, которые давались на уроках математики в школе. Мы расширили понятия операции, отойдя в сторонку от операций сложения и умножения в действительных числах. Нам не потребовались логарифмы и синусы, а непрерывные функции просто отсутствуют в дискретной математике. Разработчики ИИ, знакомые с многообразием операций над числами, находят те самые решения, которые редко связаны с десятичной системой счислений, являющейся базой для классической математики. В полях Галуа конечно число элементов, но бесконечно число самих полей Галуа.

Дискретный мир не связан с школьной математикой, хотя именно он лучше соответствует современному описанию естественного мозга. Напомню, что принятая сейчас модель нашего мозга состоит из 86 миллиардов ячеек с двумя состояниями 0 и 1. Теперь разработку ИИ можно попытаться свести к поиску тех алгоритмов, которые реализуются в биологическом мозгу, но при этом никто не мешает встраивать в эти модели ИИ то, что используется в классической математике.

Итак, в результате занятий подростки убеждаются, что интеллект выше у тех ИИ, которые были созданы специалистами со знаниями по высшей алгебре. Это в результате того, что и их собственный интеллект стал выше.