Нормальное распределение, гауссиана, закон Гаусса, который входит в систему уравнений Максвелла, метод решения уравнений Гаусса — если мы продолжим, предисловие быстро перерастет в список открытий, сделанных Карлом Гауссом, величайшим из математиков, научная жизнь которого была во много раз насыщеннее личной.
Судьба играет человеком; читая биографии, понимаешь это особенно ясно. Ребенок (девочка или мальчик, судьбе все равно) может родиться в дворянской семье, как Рене Декарт или Софья Ковалевская, в крестьянской, как Леонтий Магницкий или в фермерской, как Исаак Ньютон — но если человеку суждено стать ученым, изменить мир — с ним это случится, вопреки обстоятельствам. И жизнь профессора Карла Гаусса тому пример самый что ни на есть яркий.
Стипендия герцога Брауншвейгского
Гебхард Дидерих Гаусс, отец Карла, крестьянский сын, был садовником, каменщиком, фонтанным мастером, водопроводчиком — а еще отличался умением хорошо считать: со счетом он помогал купцам на брауншвейгских ярмарках, вел расчеты в похоронном бюро. Но все-таки большинство биографов считают, что от отца Гауссу досталось крепкое здоровье, а интеллект он унаследовал от матери, Доротеи Бенц. Умна, но неграмотна — такова была мать будущего короля математиков: она не записала дату рождения сына, но помнила, что он родился в среду, за восемь дней до Вознесения, в 1777 году, на канале Венденгребене в Брауншвейге. Через двадцать два года ее гениальный сын вычислит точную дату своего рождения (30 апреля) и попутно разработает метод определения дня Пасхи на любой год — а еще будет всю жизнь очень предан матери.

Позже, вспоминая детство, Гаусс говорил, что считать он научился раньше, чем говорить, а в три года мог найти ошибку в вычислениях отца.
В семь лет маленький Гаусс поступил в Екатерининскую народную школу. Считать там начинали учить с третьего класса, так что два года его таланты оставались нераскрытыми.
В третий класс попадали ученики разного уровня подготовки: учитель давал им разные задания, чтобы занять длинными вычислениями. Например, мог попросить посчитать сумму всех натуральных чисел от 1 до 100; и десятилетний Гаусс ответил буквально сразу после того, как учитель закончил диктовать — за это время он успел переоткрыть сумму арифметической прогрессии (и оказаться единственным, получившим верный ответ).
Иоганн Мартин Бартельс, молодой помощник учителя математики в школе (впоследствии он будет учить Лобачевского в Казани), обнаружил, как талантлив мальчик, и смог добиться для ребенка каменщика персональной стипендии от герцога Брауншвейгского — в начале XIX века покровительствовать науке хотели все властители. Мальчик иногда появлялся при дворе и поражал придворных своим искусством счета.
Правильный семнадцатиугольник
Благодаря помощи Бартельса Карлу Гауссу удалось поступить в гимназию — в одиннадцать лет. Тут он увлекся латынью, английским и французским. Изучение языков так ему нравилось и так хорошо давалось, что впоследствии он выучит и русский — по одной из легенд, чтобы читать Лобачевского в оригинале. Лингвистика настолько захватила будущего гения, что довольно долго он колебался — не мог выбрать между латынью и математикой.
С 1792 по 1795 Гаусс учился в колледже Каролинум (сегодня это технический университет Брауншвейга), посещая столько же лекций по языкам, сколько по математике; и попутно переоткрыл уже известные математические законы — метод наименьших квадратов и другие. А еще начал заниматься нормальным распределением.
Клейн, биограф Гаусса, пишет, что из любви к счету Гаусс постоянно производил над числами разные операции — умножал десятичные дроби в уме — для удовольствия, разумеется — и постепенно накопил огромный материал для наблюдений, выводов, расширив кругозор в области чисел.
В 1795, благодаря поддержке герцога, многообещающий вундеркинд поступает в Геттингенский университет — и математика наконец становится главным его увлечением. Гаусс составляет огромные таблицы простых чисел, квадратичных вычетов, результатов делений с периодами в остатке, а еще его начинает занимает зависимость периода от знаменателя. Он читает Эйлера и Лагранжа и считает, считает, считает — с прилежанием и тщанием.
В 1796 году он находит возможность построения правильного семнадцатиугольника при помощи циркуля и линейки
И попутно решает вопрос построения правильных х-угольников для определенных значений х. Гаусс гордился этим решением: он даже просил изобразить на своей могиле правильный семнадцатиугольник, вписанный в круг. Правда, убедить высечь на собственном надгробии круг и семнадцатиугольник оказалось сложнее (его там нет), чем найти решение вопроса. В итоге памятник Гауссу в Брауншвейге стоит на семнадцатиугольном постаменте — тоже вариант.
»…я случайно натолкнулся на одну изумительную арифметическую истину, и так как она не только показалась мне прекрасной сама по себе, но и навела на мысль, что она связана и с другими выдающимся фактами, я со всей энергией взялся за то, чтобы выяснить принципы, на которых она основывается, и получить строгое ее доказательство. После того как это желание, наконец, осуществилось, прелесть этих исследований настолько увлекла меня, что я уже не мог их оставить».
Карл Гаусс, «Арифметические исследования»
О «золотой теореме»
Первую запись в дневнике своих открытий Карл Гаусс сделал 30 марта 1796 года — когда он научился строить правильные х-угольники для определенных значений х. Кстати, и поныне решение этой задачи многие считают самым величайшим из сделанных математических открытий.
Гаусса не сразу поняли: например, норвежский математик Абель жаловался, что понять теорию деления круга на равные промежутки совсем не так просто; зато когда он постиг ход рассуждений Гаусса, то восхитился и назвал его гением.
Это открытие, «проба сил гауссова гения», по свидетельству его биографа, было сделано Гауссом в 18 лет!
Годы, проведенные в университете, примечательны многими открытиями Гаусса; совсем не все свои догадки он, как и Ньютон, публиковал. Например, он до Лобачевского открыл неевклидову геометрию, занимался теорией эллиптических уравнений — но результаты исследований, которые он считал незавершенными и которыми не был доволен, не печатал. Зато среди его работ не было ни одной, не отточенной до блеска или незавершенной. Собственным его девизом было «Pauca sed matura» («Немного, но зрело»).
Самой замечательной стала, без сомнения, книга «Арифметические исследования» 1801 года: арифметику Гаусс называл любимейшей наукой многих математиков и сам признавался в том, что теория чисел — его первая и главная любовь. Эта огромная (более 500 страниц!) книга содержала много результатов по теории чисел и высшей арифметике и была посвящена герцогу. Она оказала и до сих пор оказывает огромное влияние на труды по алгебраической теории чисел.
Небесная механика и потерянная Церера
В 1798 Гаусс в Гельмштадте подготовил диссертацию по основной теореме алгебры: всякий многочлен с действительными коэффициентами раскладывается в произведение многочленов первой и второй степени. Кроме того, он занимается эллиптическими функциями и изучает лемнискату Бернулли. Он долгое время не публиковал результаты своих исследований, считая, что некуда торопиться, пока в 1827 Абель и Якоби опубликовали собственные работы на эту тему.
После «Арифметических исследований» круг интересов и работ Гаусса меняется: он занимается небесной механикой (и открывает методы расчета орбит планет по малому числу наблюдений), картографией, геодезией, дифференциальной геометрией и теорией поверхностей. Кроме того, двадцатилетний Гаусс исследует элементы магнитного поля. Позже его работы станут началом теории потенциала, а ряд других работ приведут к возникновению методов статистических вычислений.
В 1799 Карл Гаусс становится приват-доцентом Брауншвейгского университета, а в 1801 (посчитайте, сколько Гауссу лет в это время?) — членом-корреспондентом Петербургской академии наук. В том же году методом вычислений он обнаруживает потерянную малую планету Цереру, это приносит ему общеевропейскую славу; а герцог увеличивает стипендию. Тем не менее, в 1801 году Гаусс перестает регулярно вести математический дневник — все основные свои математические открытия он сделал с 1796 по 1801 год, с 18 до 24 лет!
Слава Гаусса становится общеевропейской. Многие научные общества Европы дают Гассу членство, герцог увеличивает пособие, а интерес ученого к астрономии ещё более возрастает. Плюс в то время он решает жениться. Но содержать семью только на стипендию и зарплату доцента было невозможно, а вот за работу в обсерватории платили куда лучше. Гауссу даже предложили должность при Петербургской обсерватории, и он чуть не выехал в Россию; но Гумбольдт составляет ему протекцию и рекомендует профессором в Геттингенский университет.
В 1805 году Гаусс женился на Иоганне Остгоф, в то время он писал, что «жизнь представлялась ему весной со всегда новыми цветами». Это было счастливое время, но в 1809 году Иоганна и их сын умерли.

В то же время Наполеон обложил Геттинген налогом (за Гаусса его уплатил курфюрст Майнцский, друг Гете); зато увидела свет «Теория движения небесных тел», главная работа Гаусса по астрономии. В 1810 году Гаусс женился на подруге Иоганны, Минне Вальдек. В этом браке у него родятся трое детей.
Ученого продолжают чествовать и награждать премиями, а комету 1812 года везде наблюдают по расчетам Гаусса.
Гауссова кривизна
В 1820-м году Гауссу поручают геодезическую съёмку Ганновера для построения точных карт. Гаусс разрабатывает методы приложения собственных расчетов к высшей геодезии и сам проводит съемку местности — представьте себе сегодняшнего философского, к примеру, лауреата с геодезическими инструментами — буссолем, алидадой или ватерпасом в чистом поле — и удивитесь, как удивлялись современники профессора.
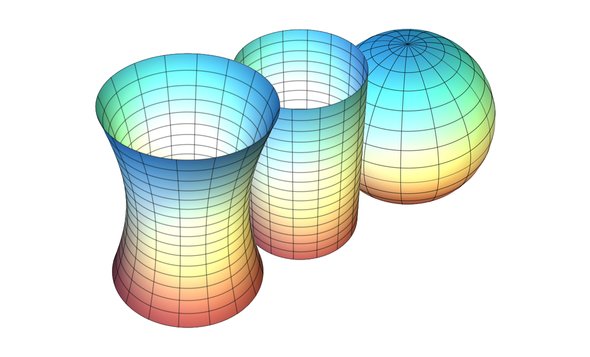
Но ученый всегда ученый: из картографической съемки ганноверских лугов и косогоров вырастает теория поверхностей, гауссова кривизна, дифференциальная геометрия — именно они в итоге вдохновят Римана на цикл работ о римановой геометрии. В то время Гаусс знакомится с работами Лобачевского и способствует избранию его почетным профессором Геттингенского университета; однако сам не публикует свои работы по неевклидовой геометрии.
«Я прихожу всё более к убеждению, что необходимость нашей геометрии не может быть доказана, по крайней мере человеческим рассудком и для человеческого рассудка. Может быть, в другой жизни мы придём к взглядам на природу пространства, которые нам теперь недоступны. До сих пор геометрию приходится ставить не в один ранг с арифметикой, существующей чисто a priori, а скорее с механикой».
Карл Фридрих Гаусс
Наконец, физика!
К концу 20-х годов почти пятидесятилетний Гаусс ищет для себя новую точку приложения сил и решает заняться физикой. Но не сразу определяется, чем именно хочет заняться: механикой, кристаллографией, электродинамикой? В 1831 году умирает Минна, его вторая жена, у Карла Фридриха начинается тяжелая бессонница, и только когда в Геттинген по личному приглашению Гаусса (они познакомились в гостях у фон Гумбольдта) перебирается молодой физик Вильгельм Вебер, у замкнутого Гаусса появляется товарищ по занятиям наукой. В Геттингене им поставлен двойной памятник.

Вебер и Гаусс занялись электродинамикой и земным магнетизмом: изобрели электромагнитный телеграф, начали разрабатывать теорию потенциала и электростатики. К сожалению, в 1837 году Вебера увольняют из Геттингена — он подписал письмо о нарушении королем конституционных свобод. В следующий раз они увидятся, тогда когда Гауссу будет 72.
В 1839 Гаусс просит Российскую академию наук прислать ему русские книги и журналы, в том числе «Капитанскую дочку» Пушкина.
Лишь в 1855, когда Гаусса не стало и был открыт его архив, стал ясен список открытий, которые он сделал до их официальных первооткрывателей.
Что Гаусс открыл, но не опубликовал при жизни
- Разработка неевклидовой геометрии до работ Лобачевского и Бойяи
- Эллиптические функции до Якоби и Абеля
- Теория кватернионов до Гамильтона
- Метод наименьших квадратов и закон распределения простых чисел до Лежандра
- В дневниках и письмах Гаусса есть заметки, которые можно счесть топологическими
«Pauca sed matura»
Что остается от человека? От Карла Фридриха Гаусса остались 21 теорема, закон методов в науке, не считая названных в его честь явлений; вулкан в Антарктиде, медаль с надписью «Король математики» и самая наивысшая награда в прикладной математике — Премия Гаусса, присуждаемая раз в четыре года Международным математическим союзом.
О Гумбольдте и Гауссе, двух замечательных немецких ученых, Даниэль Кельман написал роман «Измеряя мир», где сталкиваются два подхода — научно-исследовательский нетерпеливого и любопытного барона Александра фон Гумбольдта и сосредоточенного погружения в себя Карла Фридриха Гаусса, который замечает, что человеку для занятия наукой не нужно ничего, кроме чистого листа перед собой и сосредоточенного внимания.
«Гаусс напоминает мне образ высочайшей вершины баварского горного хребта, какой она предстает перед глазами наблюдателя, глядящего с севера. В этой горной цепи в направлении с востока на запад отдельные вершины подымаются все выше и выше, достигая предельной высоты в могучем, высящемся в центре великане; круто обрываясь, этот горный исполин сменяется низменностью новой формации, в которую на много десятков километров далеко проникают его отроги, и стекающие с него потоки несут влагу и жизнь».
Феликс Клейн
На обложке: Портрет Карла Фридриха Гаусса, 1840 год. Автор: Христиан Альбрехт Йенсен