На что обращать внимание при подготовке к профильной математике, как подступиться к сложным задачам и какими пособиями пользоваться при подготовке. Об этом на онлайн-консультации в официальной группе ЕГЭ во «ВКонтакте» рассказал Алексей Доронин — учитель математики и лауреат конкурса «Учитель года России- 2011».
ЕГЭ-2018 по профильной математике (будут сдавать 1 июня) состоит из двух частей:
- Часть первая — восемь заданий (1–8) базового уровня сложности с кратким ответом.
- Часть вторая — четыре задания (9–12) повышенного уровня сложности с кратким ответом и семь заданий (13–19) высокого уровня сложности с развёрнутым ответом.
Во время подготовки к экзамену важно не только научиться решать задачи, но и правильно рассчитать время, за которое вы эти задания выполняете. Как это сделать? Попробуйте в спокойной обстановке решить 12 первых задач из демоверсии ЕГЭ по профильной математике и посмотрите, сколько времени на это тратите. Хорошо, если у вас получается решать эти задания за 40 минут и ещё оставить 10 минут на проверку (всего на экзамен даётся 235 минут). Старайтесь придерживаться этой планки, иначе не будете успевать и рискуете сделать нелепые ошибки из-за невнимательности. Например, видите геометрическую задачу: тут же рисуете треугольник на клетчатой бумаге и на автомате начинаете вычислять площадь. А задание вообще может быть связано с нахождением средней линии, высоты, биссектрисы или медианы.
И ни в коем случае не превращайте подготовку к экзамены в нарешивание огромного количества вариантов. Надеяться на то, что вы прорешаете сто вариантов и великолепно справитесь с экзаменом — не совсем правильно. Лучше сначала сосредоточиться на решении первых 12 задач, и только после того, как поймёте, что вы без проблем решаете задания повышенной сложности, можно приступать к отработке решения самых сложных.
О том, как их выполнять и на что обращать внимание, расскажу подробнее.
Задания № 13 и 15 — проверяют, как вы решаете уравнения и неравенства
Есть много ресурсов с типовыми заданиями, где мы в разных примерах видим одно и то же неравенство. Поменяют три на пять основание логарифма, и выпускники снова и снова их решают. Но в этом году будет другое содержание части С и другое неравенство, поэтому лучше изучить разные методы решения неравенств. Тут вам поможет методический курс Шарыгина «Решение задач» — в нём очень много неравенств. Можно найти страницу, где есть показательные решения логарифмических неравенств — около тридцати вариантов. Попробуйте их все решить. Если у вас получится, то проблем на экзамене, думаю, не будет.

Ещё важно следить за вычислительной частью. Потому что арифметическая ошибка, которая повлияла на ход решения, — сразу плохо, и вряд ли задание будет вообще как-то оцениваться. Поэтому когда вы выполняете соответствующие преобразования, всё-таки смотрите, как вы находите дискриминант, как раскладываете на множитель квадратный трёхчлен. Следите за коэффициентом, за тем, как умножаете на отрицательное или положительно число, потому что именно такие нелепые ошибки приводят к неправильному ответу.

Задания № 14 и 16 — проверяют, как вы решаете задачи с геометрическими фигурами, координатами и векторами
В задачах № 14 и 16 есть пункты «а» и «б». Обычно в пункте «а» нужно доказать, в пункте «б» — вычислить. Часто ученики пытаются доказать пункт «а», вязнут в доказательстве и бросают задачу. При этом они не читают пункт «б», хотя его можно было бы решить, используя пункт «а», и получить один балл. Так было в прошлом году: те ребята, которые не смогли справиться с доказательством пункта «а», но вычислили пункт «б», получили один балл.
Часто спрашивают, нужно ли помнить названия теорем, которые используются при доказательстве. Сами названия использовать не нужно, но если вы доказываете взаимную перпендикулярность двух плоскостей, то, конечно, должны прописать условия, при которых признак перпендикулярности плоскостей срабатывает.
Формулировки вроде «прямая теорема Пифагора» или «обратная теорема Пифагора» прописывать не обязательно, потому что проверять будут именно содержание: смогли ли вы заметить те моменты, которые помогают выполнить доказательство пункта «а».

Как правильно решать стереометрическую задачу № 14? Расскажу на примере одного из своих любимых учебников «Математика: алгебра и начала математического анализа. Геометрия.10 класс» (авторы Е. В. Потоскуев и Л. И. Звавич). В конце учебника можно найти список основных теоретических фактов и посмотреть, что вы по ним знаете. Например, как доказывать перпендикулярность прямой и плоскости, как найти расстояние между скрещивающимися прямыми. На все факты, которые есть в учебниках, на экзамене можно ссылаться без доказательств. Даже если в одном учебнике описан какой-то интересный приём решения задач, а в другом — нет. Главное, чтобы учебники входили в федеральный перечень.

Задача № 17 — проверяет, как вы применяете знания на практике (тут может быть разное)
При решении задачи № 17 нужно составить математическую модель. Обычно это или уравнение, или неравенство. Иногда бывает функция, которую нужно исследовать. Здесь, скорее всего, функция будет не сложнее, чем квадратичная (из первых 12 заданий ЕГЭ). Но есть важный момент: чтобы получить один балл за решение экономической задачи, нужно прописать, что является переменной x, переменной p и переменной s. Не нужно сразу записывать в бланк само уравнение без этой преамбулы — один балл как раз и ставится за то, как вы сумели правильно составить математическую модель. На этот момент обратите особенное внимание. Даже если у вас получилось очень сложное уравнение, которое, возможно, вы не сможете решить, но составлено оно было правильно, — вы законно получите один балл.

Во всех практикоориентированных задачах, хоть в профильном экзамене, хоть в базовом, числа и значения реальные. Если у вас появляется какая-то нереальная скорость, нереальные размеры объекта, то стоит ещё раз посмотреть на решение — может быть, что-то здесь не так.
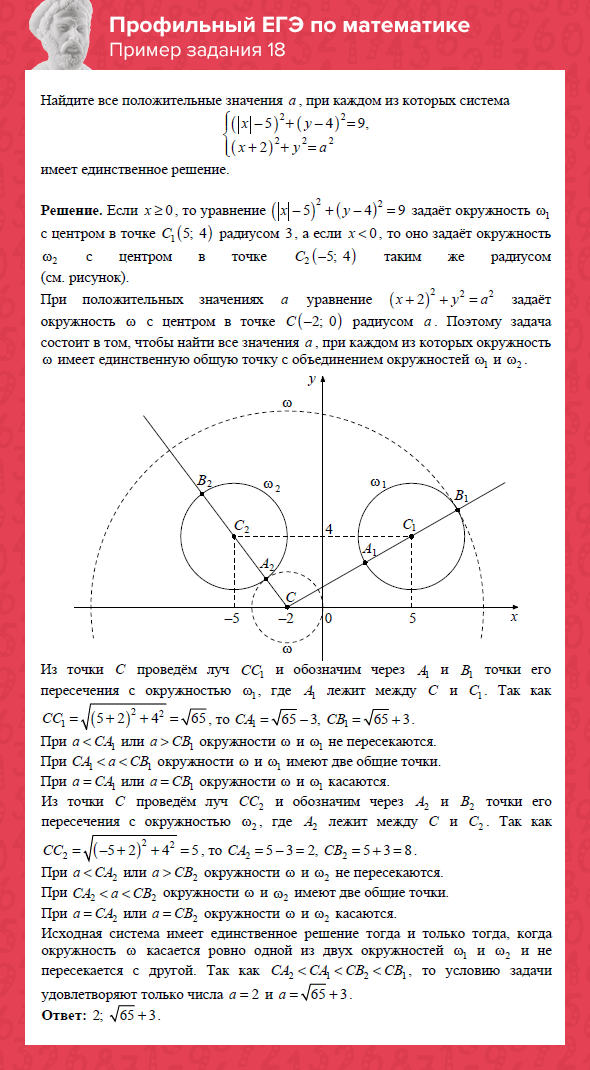
Задание № 18 — проверяет, как вы решаете уравнения и неравенства (задача с параметром)
Решение задач с параметром — вопрос сложный. Готовиться к такой задаче есть смысл, только если вы блестяще решаете все другие задачи (в том числе задание № 19). При подготовке стоит посмотреть, какие есть способы решения задачи с параметром, потому что вы можете решить 100 задач одним и тем же способом, а на экзамене будет совсем другой.
В принципе либо это аналитический способ, где задачу с параметром нужно разбить на несколько задач, либо это графический или геометрический способ, когда у вас есть некая геометрическая конструкция, и вы её анализируете. Для подготовки можно использовать замечательную книгу «Задачи с параметрами» Горнштейна. И есть совсем новый сборник «Я сдам ЕГЭ! Математика. Практикум и диагностика. Профильный уровень» И. В. Ященко.
Задание № 19 — проверяет, как вы строите и исследуете простейшие математические модели
Есть мнение, что задача № 19 — олимпиадная, но это не так. Я бы сказал, что это сложная задача школьного учебника по математике. Никаких знаний, никаких утверждений, которые касаются олимпиадной математики, вам не потребуется. В задаче есть три пункта — «а», «б», «в». В пункте «а» вам нужно будет построить пример, в пункте «б» — доказать утверждение, в пункте «в» — не только найти пример и дать ответ (например, 25), но и доказать, что больше 25 в ответе получиться не может. И не забывайте обращать внимание на формулировки «найдите натуральные числа» или «найдите целые числа» — это правда частая ошибка.

Чем пользоваться при подготовке ЕГЭ