Что такое луночки Гиппократа. Невероятная математическая история длиной в 2500 лет

В марте этого года «Мел» и матфак ВШЭ проводили конкурс на лучшую математическую статью. Мы были горды и рады, что в конкурсе приняли участие и школьники. Несколько лучших текстов, не ставших победителями, мы рекомендовали к публикации. Один из них — текст доктора наук, члена ученого совета НИУ ВШЭ Валентины Кириченко.

Год назад во время жаркого спора с коллегами я впервые услышала о луночках Гиппократа. Упомянуты они были скорее метафорически: кто-то в сердцах воскликнул, что не луночкам же Гиппократа вместо формулы Ньютона — Лейбница должны мы учить студентов на лекциях по интегральному исчислению! Хотя из контекста спора мне показалось, что луночки Гиппократа — это преданье старины глубокой, не связанное с современной математикой. И я из любопытства решила выяснить, о чем речь.

Оказалось, что за луночками Гиппократа скрывается история длиной в две с половиной тысячи лет, охватывающая самые разные страны и культуры — от берегов Эгейского моря до Альпийских гор и от Каира эпохи Фатимидов до Москвы советских времен. Особенно драматично история развивается в XX веке, а заканчивается уже в наши дни, в 2003 году.

Другой Гиппократ

Почему Гиппократ Хиосский (не тот, которого клятва) стал искать луночки, площадь которых легко вычислить? Дело в том, что он, как и многие математики до и после него, хотел найти простую формулу для площади круга. Если разбить круг на несколько удачно подобранных луночек, его площадь можно будет найти как сумму площадей этих луночек. Гиппократу удалось найти еще две подходящие луночки, но этого оказалось недостаточно, чтобы сложить полный круг. Тем не менее мысль Гиппократа заинтересовала последующие поколения математиков и поиск луночек продолжался на протяжении двух с лишним тысяч лет — разные математики пытались дополнить результаты Гиппократа и часто придумывали что-то совершенно новое и неожиданное.

Сам Гиппократ пришел в математику по довольно случайному стечению обстоятельств. Сначала он был торговцем-мореплавателем (родом он был с греческого острова Хиос, как следует из его прозвища), но его ограбили то ли пираты, то ли нечистые на руку таможенники — и он отправился в Афины искать справедливости. Вместо справедливости нашел мудрость и стал одним из ведущих афинских математиков. Ему принадлежит первая версия «Начал», которая не сохранилась, но наверняка повлияла на одноименный труд Евклида, а через него и на многие современные учебники геометрии.

Первая луночка

Гиппократ придумал три интересные криволинейные фигуры — луночки. Площадь луночки Гиппократа задается такой же простой формулой, как и площадь квадрата. Первая луночка строится так:

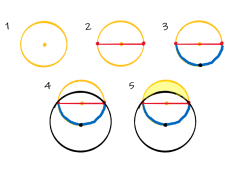
Сначала нужно построить окружность радиуса r (=жёлтая окружность на рисунке), отметить на ней концы какого-нибудь диаметра (=красный отрезок) и середину полуокружности (=синяя дуга), опирающейся на диаметр. Затем построить вторую окружность с центром в отмеченной середине дуги (черная точка) так, чтобы она прошла через отмеченные концы диаметра (красные точки). Окружности ограничивают два круга — поменьше и побольше. Луночка Гиппократа — это часть меньшего круга, которая лежит вне большего круга.

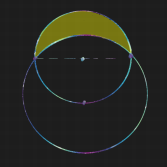
С астрономической точки зрения можно думать про меньший круг как про Луну, а про больший круг — как про тень от Земли во время неполного лунного затмения. Тогда луночка — это в точности освещенная часть Луны. Здесь читатель может остановиться и подумать над двумя вопросами. Как выразить площадь луночки через радиус r? И может ли месяц в какой-нибудь из лунных фаз совпасть по форме с луночкой Гиппократа? Ответ на первый вопрос будет дан ниже.

Площадь первой луночки

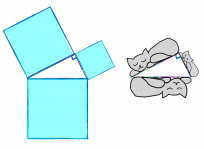
Теперь ответим на вопрос, как найти площадь первой луночки Гиппократа. Тут нам понадобится теорема Пифагора, точнее ее небольшая модификация. Теорема Пифагора утверждает, что площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах. Однако легко убедиться, что если вместо квадратов мы построим на катетах другие подобные фигуры (например, котиков), то соотношение между их площадями останется таким же. Площадь котика, построенного на гипотенузе, будет равна сумме площадей котиков, построенных на катетах. Из рисунка видно, какой смысл мы вкладываем в выражение «котик, построенный на катете».

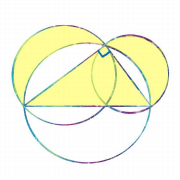
Теперь давайте возьмем равнобедренный прямоугольный треугольник и построим на его сторонах подобные сегменты круга — два синих и один красный, как на рисунке. Здесь уже явно просвечивает луночка Гиппократа.

Сумма площадей синих сегментов равна площади красного сегмента по теореме Пифагора. Отсюда видно, что луночка Гиппократа и равнобедренный прямоугольный треугольник с гипотенузой 2r равновелики (то есть имеют одну и ту же площадь), потому что луночка получается из полукруга вырезанием красного сегмента, а треугольник — вырезанием двух синих сегментов. Поэтому площадь первой луночки Гиппократа равна площади квадрата со стороной r. То, что мы только что проделали, называется квадратурой луночки. В строгом смысле слова квадрировать луночку означает построить равновеликий ей квадрат. Но вполне допускается вместо квадрата использовать другие простые фигуры, например треугольники или четырёхугольники.

Луночки Ибн аль-Хайсама

Если вам понравилось квадрировать луночки и вы хотите сами попробовать, то подумайте над задачей о луночках Ибн аль-Хайсама. Покажите, что сумма площадей жёлтых луночек на рисунке равна площади жёлтого прямоугольного треугольника (окружности построены на сторонах прямоугольного треугольника как на диаметрах). Какой именно прямоугольный треугольник взять, совершенно неважно, поэтому рисунок можно превратить в анимацию (с помощью приложения GeoGebra), подвигав вершину прямого угла. Заметим, что площадь каждой из луночек в отдельности не выражается простой формулой. Тем более интересно, что есть простая формула для их суммарной площади.

Ибн аль-Хайсам (или Alhazen в латинской транслитерации Средневековья) начал думать о луночках примерно через полторы тысячи лет после Гиппократа Хиосского — в эпоху иранского интермеццо (персидского Ренессанса). Сначала Ибн аль-Хайсам служил визирем в своем родном городе Басре, но, разочаровавшись в политике, решил посвятить жизнь науке. Он переехал в Каир, поближе к знаменитому университету аль-Азхар, и разработал проект Асуанской плотины, который очень заинтересовал египетского халифа. Однако проект нельзя было реализовать теми техническими средствами, которыми человечество располагало тысячу лет назад. Ибн аль-Хайсаму пришлось около десяти лет то ли скрываться от гнева халифа, то ли сидеть под домашним арестом, изображая сумасшедшего, а все его имущество было конфисковано. Именно в этот период он написал фундаментальный труд о теории света и зрения, за что получил прозвище «отец современной оптики».

Вторая и четвертая луночки

Как уже говорилось, Гиппократ построил еще две квадрируемые луночки. Давайте попытаемся восстановить ход его мысли. Секрет успеха первой луночки в том, что ее площадь по построению оказалась равна площади треугольника. Можно попробовать повторить рассуждение, заменив треугольник на четырёхугольник или пятиугольник. Более общо — впишем в окружность «пифагоров» многоугольник, у которого одна сторона (условная гипотенуза) длиннее остальных, все остальные стороны равны друг другу, и выполняется «теорема Пифагора»: сумма квадратов коротких сторон равна квадрату длинной стороны. По такому многоугольнику можно построить луночку, площадь которой равна площади «пифагорова» многоугольника. Детали конструкции для треугольника (это уже знакомая нам первая луночка Гиппократа), четырехугольника и шестиугольника приводятся на рисунке.

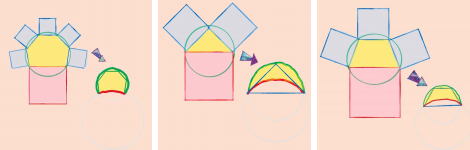
Мы построили три квадрируемые луночки, причем первая совпадает с первой луночкой Гиппократа. Вторая луночка совпадает с его же второй луночкой. А вот луночка, связанная с «пифагоровым» шестиугольником, была построена на две с лишним тысячи лет позже Гиппократа: ее построил Даниэль Вийнквист в 1766 году (поэтому эту луночку мы будем называть четвертой луночкой Гиппократа, а не третьей).

Наша историческая реконструкция мысли Гиппократа не соответствует реальному ходу истории

На первый взгляд история кажется невероятной: неужели понадобились тысячелетия, чтобы обобщить «пифагоров» четырехугольник до «пифагорова» шестиугольника? Тут надо пояснить, какой смысл древнегреческие математики вкладывали в понятие построения. У них были очень точные правила игры: построить означало построить с помощью циркуля и линейки, и никак иначе. Мы не знаем, появились ли эти правила уже во времена Гиппократа Хиосского, но это предположение кажется правдоподобным. Во всяком случае, в эпоху Евклида правила построения циркулем и линейкой четко оформились (в наши дни научиться играть по правилам можно в приложении Euclidea). Построить циркулем и линейкой вписанный в окружность «пифагоров» четырёхугольник не очень сложно (попробуйте это сделать). Догадаться же до построения вписанного «пифагорова» шестиугольника без алгебры вряд ли возможно (а с пятиугольником и того хуже: его вовсе нельзя построить, но это мы забегаем вперёд). Похожая история произошла с построением правильного 17-угольника (его построил Гаусс в 1796 году), хотя сама задача несомненно интересовала древнегреческих геометров, идеи ее решения лежали далеко за пределами античной математики.

Третья и пятая луночки

В своей кандидатской диссертации Даниэль Вийнквист (под научным руководством Валлениуса) построил пять луночек Гиппократа — три ранее известных (на рисунке обозначены Fig1, Fig3, Fig4) и две новых (Fig5 и Fig6). Для иллюстрации приводим две страницы из диссертации Вийнквиста. Слева — алгебраические вычисления для четвёртой луночки (Fig5), а справа — геометрические построения всех пяти луночек Гиппократа (между ними затесались и луночки Ибн аль-Хайсама — куда ж без них). Конечно, как и с четвертой луночкой, главная сложность с пятой луночкой в том, чтобы построить ее циркулем и линейкой. Видна польза алгебры: если в статье Ибн аль-Хайсама не владеющие арабским читатели могут понять только чертеж, то в диссертации Вийнквиста не владеющие латынью вполне могут догадаться (из последней строчки на стр. 20), что длины AE, AF, EF пропорциональны 1, √5, √1 +12√5 +12√25 + 20√5, соответственно. Последняя формула — с тремя вложенными корнями — даёт некоторое представление о том, почему четвёртую луночку существенно сложнее построить циркулем и линейкой, чем первые три.

Страницы из диссертации Вийнквиста

Результаты Вийнквиста переоткрывались несколько раз. В 1840 году это проделал Томас Клаузен, слышавший лишь о первой луночке Гиппократа. Клаузен сумел заинтересовать математическое сообщество новой гипотезой (гипотеза Эйлера — Клаузена) — он предположил, что никаких других квадрируемых луночек циркулем и линейкой построить нельзя.

Клаузен родился в рыбацкой деревне Сногбек в бедной семье, с детства работал, поэтому в школу не ходил и был неграмотным. В двенадцать лет он устроился пастухом к пастору в соседнем приходе. Пастор заметил, что мальчик необыкновенно умен, и разрешил ему совмещать выпас скота с учебой в школе. Кроме того, пастор учил Клаузена астрономии и математике, поскольку сам увлекался этими науками. Блестяще окончив школу, Клаузен по протекции пастора устроился секретарем в обсерваторию в Альтоне, где познакомился с Гауссом, проводившим поблизости от Альтоны геодезические измерения. Гаусс оценил способности молодого человека, что оказалось очень кстати, когда начальник обсерватории уволил Клаузена (они плохо ладили, и последней каплей стал разбитый Клаузеном дорогой барометр). Клаузен отправился в Гёттинген к Гауссу и попросил его замолвить словечко перед шефом. Не в силах отказать Гауссу, начальник обсерватории снова принял Клаузена на работу, но тот, как назло, влюбился в племянницу начальника.

Следующие пятнадцать лет жизни Клаузена могли бы стать сюжетом для одной из самых грустных сказок его соотечественника Ганса Христиана Андерсена. Тем не менее Клаузен продолжал заниматься математикой и астрономией и в 1842 году (когда ему было уже за сорок) получил позицию профессора астрономии в Дерптской обсерватории. Спустя ещё два года Кёнигсбергский университет присудил ему почётную степень — к нему наконец начали относиться в соответствии с его талантами и достижениями. Хотя Клаузен зарабатывал на жизнь астрономией, главным интересом его жизни была чистая математика. Он получил соблазнительное предложение из Пулковской обсерватории, но предпочел остаться в Дерпте (современном Тарту).

Луночки Гиппократа в XX веке и в наши дни

Итак, в XIX веке было известно пять луночек Гиппократа. Вот они все на одном рисунке: луночки жёлтые, а сиреневым закрашены «наконечники», площади которых совпадают с площадями луночек.

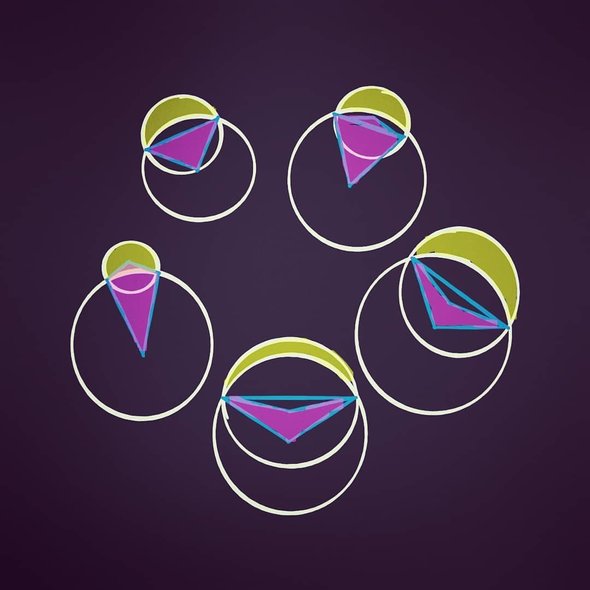
Мы так и не ответили на вопрос, верна или неверна гипотеза Эйлера — Клаузена. Может быть, надо подождать ещё пару тысяч лет и какой-нибудь марсианский математик построит неизвестную науке луночку Гиппократа? Оказывается, что нет, не построит, хотя убедительно объяснить невозможность такого построения совсем не просто.

История с гипотезой Эйлера — Клаузена довольно запутанная и заслуживает отдельного рассказа. Как и другие «задачи о невозможном», уходящие корнями в античную математику, гипотеза стала испытательным полигоном для математических методов, развитых в XIX веке. Но орешек оказался крепче, чем классические задачи о невозможности удвоения куба, трисекции угла и квадратуры круга. Действительно, невозможность удвоения куба и трисекции угла вполне можно объяснить старшекласснику, умеющему делить многочлены с остатком (см. заочную часть проекта «Алгебраические числа как векторы» на Летней конференции «Турнира городов»), а невозможность квадратуры круга (или трансцендентность числа π) — первокурснику, овладевшему основными понятиями математического анализа (см. видеоролик «Доказательство: e и π — трансцендентные числа» канала Mathologer). Однако для доказательства невозможности построения или квадратуры каждой луночки, отличной от пяти луночек Гиппократа, нужна более тяжелая артиллерия.

Двойной удар по гипотезе Эйлера — Клаузена был нанесён в 1934 году с разных сторон: алгебраической (в работе Николая Чеботарёва) и трансцендентной (в работе Александра Гельфонда). Но если Чеботарёв явно решал задачу о луночках, то Гельфонд решил седьмую проблему Гильберта, в которой о луночках не было ни слова. Только в 2003 году Курт Гирстмейр заметил, что результат Гельфонда и его обобщение, полученное Аланом Бейкером (1966), вместе с результатом Чеботарёва, дополненным его учеником Анатолием Дородновым (1947), дают полное доказательство гипотезы Эйлера — Клаузена.

Хотя гипотеза Эйлера — Клаузена стала доказанной теоремой, это вовсе не означает, что математики перестали думать о луночках Гиппократа. Например, в видеоролике «Lunes» канала Numberphile можно увидеть, как красиво думает о луночках Барри Мазур. В частности, он придумал квадрировать луночку с помощью «наконечника» и строить «пифагоровы» многоугольники (только он их называет «гиппократовыми»). Мораль истории ясна: хорошую математическую мысль интересно думать во все времена.