Проблемы ФГОС-2019: как (не) выучить математику в 5–6-м классах

Учителя часто выражают недовольство, что им приходится следовать Стандарту, который, по мнению многих, не имеет содержания. До конца года планируют принять новый ФГОС. Наш блогер, учитель математики и автор учебников Александр Шевкин, поделился своим мнением о новом образовательном стандарте по математике и объяснил, чем он плох.
Сначала рассмотрим материалы проекта ФГОС ООО (далее: Стандарт), относящиеся к изучению математики в 5–9-м классах, которые называют первым-пятым годами обучения. Шестнадцать требований пункта 38 написаны одним предложением. Читается тяжело, но чуть легче, чем в апрельском варианте Стандарта: критика подействовала.
«38. Предметные результаты освоения основной образовательной программы основного общего образования… ориентированы на применение знаний, умений и навыков обучающимися в учебных ситуациях и в реальных жизненных условиях, а также на успешное обучение на следующем уровне общего образования и должны обеспечивать…»
Канцелярит ещё тот: основная образовательная программа основного общего образования! Речь идёт о применении знаний, умений и навыков учащимися, а не знаний учащихся (обучающимися — это для учёности). Главное здесь: учащиеся будут применять не свои знания, которыми не владеют! Нигде не говорится, должны ли учащиеся получать знания в процессе обучения. Речь идёт только о применении знаний, так как описаны требования к предметным результатам, выносимым на контроль (это уточнят ниже). Таким образом, Стандарт не определяет содержание обучения, не направляет процесс обучения, он фиксирует только то, что выносят на контроль.
Эффект использования Стандарта будет таким: требования к результатам обучения, выносимым на контроль, станут требованиями и к процессу обучения, и к учебникам. Учитывая, что на контроль выносится не всё, изучать станут только то, что контролируется. Так произошло с геометрией. Сначала отменили устный экзамен, после этого отпала необходимость доказывать теоремы — что не требуют на контроле, то не нужно ни детям, ни родителям, ни даже учителям! Если требуют только применение знаний, то из учебного процесса исчезает требование давать школьникам полноценные знания в системе, научить их доказывать хотя бы несколько простых фактов, теорем. На ОГЭ и ЕГЭ учащиеся «получают знания для применения» — официальную шпаргалку.
Авторы документа оказались заложниками ошибочной идеи поставить деятельность выше содержания обучения
Они описывают требования не к тому, что надо преподавать в школе (в терминах содержания обучения), а к тому, что будут проверять на выходе. Да ещё в терминах деятельности. Их каждый будет понимать по-своему. В пункте 2 есть требование: «Предметные результаты… должны обеспечивать… умения оперировать понятиями: натуральное число, простое и составное число…»
Включает ли это «оперирование» действия с натуральными числами? Какие? Простые и составные числа не входят в понятие натуральное число, раз выписаны отдельно? Разве это допустимо для закона? Читаем пункты, относящиеся к 5–9-му классам (п. 38.5).
«Предметные результаты… должны обеспечивать:
2) умения оперировать понятиями: натуральное число, простое и составное число, делимость чисел, целое число, модуль числа, обыкновенная дробь, десятичная дробь; стандартный вид числа; рациональное число, иррациональное число, арифметический квадратный корень; выполнять действия с рациональными и иррациональными числами; сравнивать числа, упорядочивать числа; представлять числа на координатной прямой; округлять числа; делать прикидку и оценку результата вычислений; умение оперировать понятиями: множество натуральных, множество целых, множество рациональных, множество действительных чисел…»
Здесь многое не упомянуто, например возведение числа в степень, квадратный корень — он бывает не только арифметический. Но уж сравнение чисел всегда изучают до действий с ними. Лучше поменять порядок.
В пункте 3 речь идёт об умениях, связанных с буквенными выражениями, но термин «буквенные выражения» не используется. Это отражение попытки лет 50 тому назад ввести понятие «выражение с переменной» с таким широким толкованием, что в одном учебнике, который я рецензировал для Федерального экспертного совета Минпроса СССР много позже, было задание: «К доске пойдёт х…» Художник нарисовал девочку, держащую под мышкой голову мальчика (или наоборот) — это для быстрой смены «значения» х. Авторов учебника «шалость» художника не смутила.
Пропущен одночлен, действия с буквенными выражениями всех перечисленных видов. Требуют использовать формулы сокращённого умножения, а знать или доказывать эти формулы надо? Так как на экзамене будет шпаргалка, то ни знать, ни доказывать не надо, надо использовать. Требуется выполнять несложные преобразования целых выражений; дробно-рациональных выражений и выражений с квадратными корнями.
Настораживает стремление авторов минимизировать применение устоявшейся школьной терминологии
Про буквенные выражения и одночлены сказано выше. Оборот «выражения с квадратными корнями» неудачно заменяет «иррациональные выражения». Это попытка свести всё к квадратным корням — длинно и ошибочно, так как сумма квадратного корня и кубического корня тоже выражение с квадратными корнями. Учащиеся знают, что есть рациональные числа и иррациональные числа. Почему бы, опираясь на эти знания, не назвать буквенные выражения рациональными и иррациональными? Если уж пишете выражения с квадратными корнями, то будьте последовательны: пишите «выражения с числами и буквами». Будет в одной стилистике — ниже уровня церковно-приходской школы.
Про дробно-рациональные выражения, дробно-рациональные уравнения и дробно-рациональные неравенства надо бы писать короче: без первого слова «дробно», которое ничего не добавляет и не убавляет, а только мешает — рациональные выражения, рациональные уравнения и рациональные неравенства. Потом будут иррациональные выражения, иррациональные уравнения и иррациональные неравенства.
В пункте 4 числовое равенство и числовое неравенство несколько запоздали. Разве это не числовой материал из пункта 2? Понятия встретились впервые, то есть при изучении чисел они не использовались?
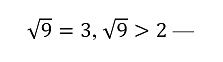
Про уравнения и неравенства нельзя оставлять единственный подход: уравнение и неравенство с переменной. До внедрения функционального подхода говорили про уравнения и неравенства с неизвестным. Давайте вспомним задачу про фазанов и кроликов и её решение с помощью уравнения. Если фазаны не убегают из клетки, для ученика число фазанов (x) в уравнении переменная величина или постоянная, но пока неизвестная?
Говорить про переменные стали 50 лет назад ради более раннего введения функции — это не математика вопроса, а забота о подготовке к введению понятия «функция». За 50 лет к раннему появлению функции учителя привыкли, но продолжили говорить о переменной. Давайте допустим второй подход, скажем: уравнение с переменной (с неизвестным).
В пункте 5 надо бы уточнить: не «функция, график функции, аргумент и значение функции», а «аргумент, функция, значение аргумента и значение функции, график функции». Про наибольшее и наименьшее значения функции лучше добавить: на промежутке.
В пункте 6 потеряна бесконечно убывающая геометрическая прогрессия. Так и не учтено апрельское замечание: не сумма n первых членов (n слагаемых, каждое из которых — первый член прогрессии), а сумма первых n членов.
В пункте 7 сказано про арифметический способ решения текстовых задач, но не указаны классические типы таких задач — на движение, на части, на нахождение двух чисел по их сумме и разности, на дроби (зачем там доли?), на совместную работу, на прямую и обратную пропорциональность, на проценты, на смеси и сплавы. Нет в методике математики таких типов задач «на цену товаров и стоимость покупок и услуг, налоги, задачи из области управления личными и семейными финансами». Это разные сюжеты задач на связь трёх величин: цена, количество, стоимость. Так раньше и писали в обруганных советских программах по математике, к которым мы неизбежно вернёмся, когда после долгих поисков нового лица российской школы надо будет выходить из пустыни «реформ» и начинать ликвидацию безграмотности на всех уровнях.
В пункте 8 меня смутило требование решать простейшие комбинаторные задачи методом прямого и организованного перебора — это научная терминология или учительские жаргонизмы? Перебор бывает непрямой? Организованный перебор можно назвать упорядоченным перебором? Прилагательные лучше снять. Почему упомянуто только правило умножения? Есть ещё и правило сложения.
В пункте 9: «иметь представление о роли закона больших чисел в массовых явлениях» — перебор. Сказать об этом в 10–11-м классах будет совсем не поздно.
В пункте 10: «решать задачи на нахождение геометрических величин» — пропущено слово «значений». Опять требуется применять геометрические факты, использовать свойства геометрических фигур для решения задач, а доказываются ли факты, свойства, признаки (они не упомянуты) — понимайте как вам удобнее.
Нагрузили геометрию стереометрией, а в пункте 11 выбросили всю геометрию, связанную с окружностью
В пункте 12 не учтено апрельское замечание, что длина (отрезка) и расстояние (между его концами) — одно и то же. Опять применение формул, теоремы Пифагора, теоремы косинусов, теоремы синусов. А теорему Фалеса, теорему о пропорциональных отрезках и многие другие теоремы применять не будем? Про знание этих теорем и не заикаюсь.
В пункте 15 упорно теряется разность векторов — с апреля.
Грустное чтение получилось по пункту 38.5. Полное впечатление, что это никому не нужное заполнение шаблона. Во всяком случае, трудно представить, как и зачем эту часть Стандарта можно применить в школе.
Проект ФГОС начального и основного общего образования.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.















