5 тезисов о красоте и простоте математики. Даже если вы считаете, что «это не моё»
19.04.2021
Когда вы в последний раз сталкивались с математикой? Скорее всего, в школе, и, скорее всего, запомнили только занудные уроки, бесконечные примеры и бесполезные задачи. Но такова ли математика по своей сути? Пробуем разобраться вместе со студенткой второго курса матфака НИУ ВШЭ Вероникой Треумовой.
1. Математика — это для избранных
В большинстве случаев от математики отмахиваются со словами: «Это не моё!» — почему-то считается, что это занятие подходит только самым одаренным и талантливым. Но так ли это на самом деле?
Прежде чем ответить на этот вопрос, давайте подумаем, откуда вообще взялась математика. Представим себя в роли древнего человека, познающего мир. И первый вопрос, который мы себе зададим, будет «сколько?». Сколько пальцев на руках, сколько лепестков у розы, сколько монет в мешке, сколько звёзд на небе? Появляются цифры. Далее возникают вопросы более сложного толка — каких предметов больше, а каких меньше? А на сколько?
Впрочем, даже древних людей интересовала не только арифметика. Давайте вспомним древнегреческую легенду об измерении Фалесом Милетским высоты египетских пирамид. Она иллюстрирует названную его именем теорему из школьной геометрии, известную каждому: «Учёный поставил шест на край отбрасываемой пирамидой тени. Измерив длину шеста и его тени, он показал, что отношение длины тени пирамиды, сложенной с половиной длины основания, к тени от шеста равно отношению высоты пирамиды к высоте шеста».

Идеи идеальных абстракций тоже находятся во внешнем мире. Яблоко напоминает нам сферу, гладь озера — плоскость, а крылья бабочки — равные треугольники. «Природа разговаривает с нами на языке математики», — пишет Галилей.
То есть оказывается, что математические задачи естественным образом возникают и в природе, и в нашей жизни. А мы интуитивно понимаем, как всё это работает. Иными словами, мы уже живём с математикой внутри и наша задача состоит лишь в том, чтобы открыть ее в себе и в окружающем мире. Таким образом, все мы в той или иной степени имеем способности к математике просто потому, что мы люди.
2. Математика — это сложные формулы и непонятные слова
Любой человек при слове «математика» представляет себе набор формул, составленных из странных символов, а словосочетание «гиперболический параболоид» приводит многих из нас в смертельный ужас.
На самом деле, математический формализм — всего лишь универсальный язык, который был изобретён для удобства: это способ оформить свои идеи, мысли, соображения, записать их так, чтобы коллеги — не только математики, но и инженеры, информатики, физики, химики, экономисты и социологи — из дальних стран или даже из другой эпохи смогли прочитать их, понять и использовать. В каком-то смысле это такой же язык, как русский или английский, и он выполняет те же функции. Это перевод с нашего внутреннего языка, подлежащий единственной трактовке. Давайте попробуем «перевести» следующее:
Площадь треугольника является инвариантом по отношению к изометриям плоскости
Начнём с инварианта: (от лат. invarians — «неизменяющийся») это величина, остающаяся неизменяемой при тех или иных преобразованиях. Можно запомнить так: in — приставка «не» в английском языке, vary — «варьироваться, меняться». Это понятие играет ключевую роль в математике; множество глубоких теорий имеет своей целью поиск инвариантов. Что касается изометрии (древнегреческий ἴσος — «равный» + μετρέω — «измеряю»), то это такое преобразование плоскости, которое сохраняет расстояния. Например, растяжение не обладает этим свойством, а поворот — да.
Так что же здесь, по сути, сказано? Представьте, что на листе бумаги нарисован треугольник. Как бы вы ни крутили или ни переворачивали этот лист, площадь треугольника будет оставаться прежней, так как она выражается через длины сторон (формула Герона). Да, всё очень просто!
Тех, кто испугался в начале пункта, уверяю, в гиперболическом параболоиде нет ничего страшного — это всего лишь поверхность в трёхмерном пространстве (проще — в нашем мире), которая напоминает седло или кусочек Pringles и описывается уравнением
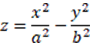
(то есть все тройки точек с координатами, которые ему удовлетворяют, будут лежать на поверхности). Своим названием он частично обязан тому факту, что на нём лежат и гиперболы, и параболы (пересечения с горизонтальными и вертикальными плоскостями, соответственно).

На самом деле, связь геометрических объектов и алгебраических уравнений поражала не одно поколение учёных-математиков. Десятилетний Александр Гротендик (один из величайших математиков XX века) остро отреагировал и испытал настоящее озарение, когда понял, что окружность, этот совершенный геометрический предмет, может быть в точности описана элегантной формулой

Остановитесь и задумайтесь, разве не чудо? Математика призвана раскрывать красоту мышления, рассуждений и логических построений. Она учит видеть чудеса. Нужно лишь рассмотреть конкретные идеи за этим нагромождением переменных, интегралов и определений, уловить полёт мысли авторов.
3. Математика — это скучно
Сидеть и часами решать задачи иному привидится лишь в кошмаре. Куда более увлекательными детям кажутся игры. Но множество игр — как детских, так и взрослых — описываются математическими моделями. Математика помогает находить выигрышные стратегии, строить закономерности, оценивать вероятности.
Знали ли вы, что в крестики-нолики при правильной игре первого игрока второй выиграть не сможет (если нет, обдумайте это)? А слышали, что в настольной игре доббль используются концепции из проективной геометрии?
Попробуйте сыграть с детьми в такую игру: нарисуйте шоколадку с плитками 3*5 или даже возьмите настоящую. Двое по очереди её ломают. За ход разрешается сделать прямолинейный разлом любого из кусков вдоль углубления. Проигрывает тот, кто не сможет сделать ход. Сыграйте несколько раз, можно менять размеры шоколадки. На самом деле, это задача-шутка! Подумайте почему.
Или, возможно, такая игра сможет привлечь ваше внимание: насыпьте две кучи камней, по семь в каждой. За ход разрешается взять любое количество камней, но только из одной кучки. Проигрывает тот, кому нечего брать. В этой игре есть выигрышная стратегия, называемая «симметричная». Вы наверняка догадаетесь, в чём она состоит.
Однако математика не просто применима в области каких бы то ни было игр. Она сама является своего рода игрой. Да-да! Игрой в уравнения, функции, кривые, фигуры. Многие великие учёные, по сути, строили теории или давали ответы на те или иные вопросы исходя из совершенно детского, искреннего любопытства. Они открывали законы, выявляли некоторые свойства, устанавливали связи, играя. Причём правила здесь задаёт логика и здравый смысл.
Таким образом, столкнувшись с трудной задачкой, можно отнестись к ней как к игре. Попробовать тот или иной способ, сделать нестандартный ход, изобрести хитрый трюк. И тогда вечер, проведённый за решением задач, превратится чуть ли не в самый захватывающий в вашей жизни.
4. Математика — это то, что трудно представить
Как бы не так! В математике, поверьте, очень много красивых картинок; она наглядна. Математика точно так же, как и рисование, развивает воображение и пространственное мышление. Есть много способов убедиться в этом на практике, я приведу лишь несколько.
В математике весьма популярны доказательства методом «смотри на картинку». Им пользовались, например, в Древней Индии — сопровождали утверждения только изображением с подписью «Смотри».
«Радость математического открытия, — писал Андрей Колмогоров, — я познал рано, подметив в возрасте пяти-шести лет закономерность:
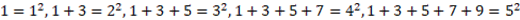
и так далее». Закономерность эта была известна еще в Древней Греции за 500 лет до нашей эры.
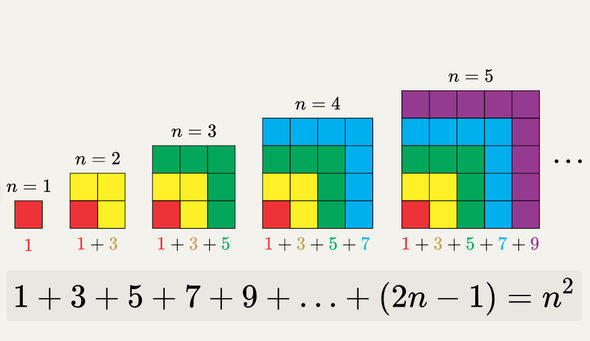
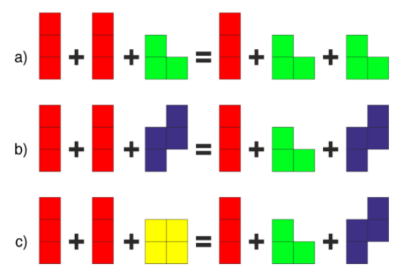
Несомненно, больше всего картинок предоставляет геометрия. Например, с младшими детьми можно заниматься фигурами на плоскости, а также графами. Детей могут увлечь задачи на разрезы и склейки фигур, пентамино. Например, найдите фигуру, которую можно сложить из указанных фигур. Фигуры можно вращать и переворачивать, но нельзя накладывать.
Что касается графов, здесь тоже очень много интересных задач. Испытайте себя в такой:
На кошачьей выставке каждый посетитель погладил ровно трех кошек. При этом оказалось, что каждую кошку погладили ровно три посетителя. Докажите, что посетителей было ровно столько же, сколько кошек.
С ребятами постарше можно осваивать и геометрию трёхмерных объектов. Посильна вам, например, такая задачка? Арбуз разрезали на 4 части и съели. При этом корок оказалось 5. Как такое может быть? Ответ и другие интересные задачки можно посмотреть здесь.
Понять, как устроены правильные многогранники (октаэдр, додекаэдр, икосаэдр) можно, склеивая их самостоятельно.

Попробуйте склеить ленту Мёбиуса из листа бумаги, раскрасить ее в 2 цвета. (не получится, потому что на самом деле у нее лишь одна сторона). Нарисуйте посередине замкнутую линию и разрежьте по ней — вы снова получите ленту Мёбиуса.
Рассмотрите бублик (тор, как его называют математики) и попробуйте найти на нём 3 семейства окружностей (как пересечения с плоскостями).


Нижняя картинка впоследствии (уже во «взрослой» математике) приводит к фундаментальному и нетривиальному понятию, а именно к расслоению Хопфа.
Визуализация математических сюжетов помогает лучше их осознать, прийти к интуитивному пониманию. Это возможность почувствовать математику, буквально прикоснуться к ней руками. В дальнейшем абстрактное мышление может пригодиться в самых разных ситуациях, как бытовых, так и профессиональных, когда необходимо будет мыслить нестандартно, приходить к неочевидным решениям. А умение создавать в уме чёткий образ, несомненно, необходимо каждому.
5. Математика — это огромный таинственный сад
Математику можно представлять себе как гору, которую вы, бесстрашный альпинист, с упорством покоряете изо дня в день. Единственное, у этой горы нет вершины: возможности познания в математике бесконечны.
Итак, мы убедились в том, что математика может быть нестрашной и даже интересной при смене ракурса. Математика многогранна; связывая множество различных областей знания, она помогает найти гармонию в мире, создать стройную, цельную его картину.
Но одно из главных качеств математики — это возможность испытывать ни с чем не сравнимое удовольствие от очередной победы над задачей. Поверьте, это очень здорово — испытывать радость открытия, сделанного собственными руками. И пусть люди уже нашли решение сотни лет назад — это неважно, ведь математика — это огромный таинственный сад, где к каждому утверждению с разных сторон ведёт множество тропинок. То есть ваше рассуждение, скорее всего, будет отличаться от решения другого человека. Разве после этого могут остаться сомнения в том, стоит ли увлекаться математикой?
Фото на обложке: Shutterstock / alphaspirit.it














