А вы готовы к профильному ЕГЭ по математике? Разбираем типичные ошибки

Совсем скоро выпускники будут сдавать профильный ЕГЭ по математике. Обязательный ЕГЭ по математике разделили на профильный и базовый в 2016 году. Самое время напомнить о его структуре, а также об основных ошибках, которые допускают ученики. Программист и учитель математики Тимур Гуев подготовил для выпускников гид по экзамену с разбором типичных ошибок.

Единый государственный экзамен по математике сдают обязательно. Базовый ЕГЭ можно сдать уже в 10 классе. Он нужен тем школьниками, которые поступают по специальностям, не связанным с математикой. Профильную математику сдают те, кому она так или иначе необходима для поступления. Мы поговорим именно о профильном ЕГЭ.

Минимальный балл по математике — 27. Вузы не могут устанавливать проходной порог ниже этого уровня. Чтобы набрать эти баллы, нужно выполнить шесть заданий. Первая часть содержит восемь заданий, где требуется записать краткий ответ в виде целого числа или конечной десятичной дроби. Во второй части четыре задания с кратким ответом и семь заданий, в которых требуется записать полный и обоснованный ответ на поставленную задачу. На выполнение экзаменационной работы отводится 3 часа 55 минут (235 минут). С собой можно взять лишь простую линейку. В профильный КИМ по математике включаются справочные материалы –основные тригонометрические тождества.

Задание 1 — применение математических знаний в повседневной жизни

Ошибки: арифметические просчёты, неправильное округление чисел. Школьники часто путаются, в большую или меньшую сторону нужно округлить полученный ответ. Рассмотрим примеры.

Задача 1. Сырок стоит 7 рублей 20 копеек. Какое наибольшее число сырков можно купить на 60 рублей?

Решение. Поделив 60 на 7,2, мы получим 8 целых и 1/3. Мы можем купить только 8 сырков, поскольку на 9 сырков не хватает денег. Поэтому производим округление в меньшую сторону — его ещё называют округлением с недостатком.

А вот другой пример.

Задача 2. В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какого наименьшего количества пачек бумаги хватит на 4 недели?

Решение. За 4 недели будет израсходовано 4 · 1200 = 4800. Так как в пачке 500 листов, нам потребуется 4800/500 = 9,6 пачек бумаги. Но здесь уже нужно округлять в большую сторону, то есть правильный ответ 10. Мы округлили с избытком.

Также необходимо помнить основное правило округления числа до целого (до единиц). Для этого нужно отбросить запятую и все числа после неё.

Правило округления до целого. Если первая из отброшенных цифр 0, 1, 2, 3 или 4, то число не изменится. Если первая из отброшенных цифр 5, 6, 7, 8 или 9, предыдущую цифру нужно увеличить на единицу.

Например, число 6,3 мы округлим до 6, а число 6,8 — до 7.

Задача 3. Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого.

Решение. Диагональ телевизора в сантиметрах равна 64 · 2,54 = 162,56. Так как первая цифра после запятой = 5, то увеличиваем предыдущую цифру на единицу и получаем 163. Это и есть ответ.

Задание 2 — работа с графиком, построенным по некоторым данным

Ошибки: невнимательное чтение условий.

Задача. На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизотали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 28 мая. Ответ дайте в градусах Цельсия.

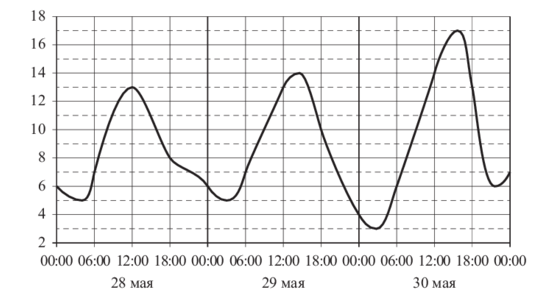
Решение. Необходимо обращать внимание на ключевые слова: наибольшее или наименьшее, а также на день, в который требуется определить искомое значение. Многие ученики просто берут самую нижнюю точку графика и пишут в ответе «3». Однако в условии задачи нужно найти наименьшую температуру именно 28 мая! А значит, правильный ответ 5.

Задание 3 — действия с геометрическими фигурами

Ошибки: в задачах с окружностями.

В этом типе задач, как правило, требуется найти площадь, периметр, расстояние или градусную меру угла. Важно помнить формулы площадей основных геометрических фигур: квадрата, треугольника, прямоугольника, параллелограмма, трапеции, ромба и круга.

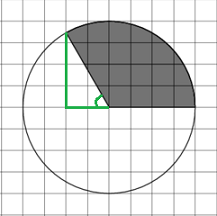
Задача 1. На клетчатой бумаге с размером 1×1 изображена окружность и вписанный в неё острый угол. Найдите градусную меру дуги окружности, на которую опирается этот угол. Ответ дайте в градусах.

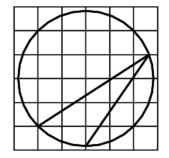
Решение. Для решения этой задачи нужно знать теорему о связи градусной меры вписанного и центрального угла, опирающихся на одну дугу. В нашем случае центральный угол, опирающийся на нужную дугу (выделен зелёным цветом), равен 45°. Поскольку величина дуги измеряется величиной её центрального угла, то это и есть ответ.

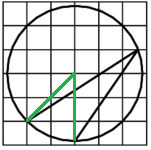
Ещё один пример.

Задача 2. На клетчатой бумаге изображен круг. Какова площадь круга, если площадь закрашенного сектора равна 32?

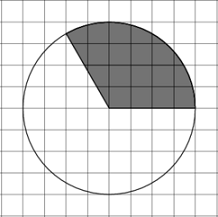
Решение. Несложно заметить, что угол, смежный с центральным углом, изображенным на рисунке, равен 60°, поскольку его косинус равен ½. Значит, закрашенный центральный угол равен 180° — 60° = 120°. Поскольку в полном обороте 360°, то искомый ответ в три раза больше площади указанного сектора. То есть площадь круга равна 96.

Задание 4 — теория вероятности

Ошибки: невнимательное чтение условий.

Задача. На экзамен вынесено 60 вопросов, Тимур не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный вопрос.

Решение. Очевидно, Тимур выучил 57 вопросов, а значит, искомая вероятность равна 57/60 = 0,95.

Многие ученики вместо этого делят 3 на 60 и получают ответ 0,05, то есть высчитывают вероятность того, что Тимуру попадётся невыученный билет.

Задание 5 — простейшее уравнение

Ошибки: не учесть ОДЗ уравнения.

Задача. Решите уравнение

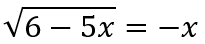
Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение. Такое иррациональное уравнение решается возведением обеих его частей в квадрат. Тут-то и кроется ошибка. Такое возведение не является равносильным, а значит, могут появиться посторонние корни. Впрочем, их легко обнаружить. Корни квадратного уравнения, полученного после возведения обеих частей уравнения в квадрат, равны x = -6, x = 1. Очевидно, положительный корень нам не подходит, так как правая часть исходного уравнения будет отрицательной. Значит, ответом на задачу является число -6.

Задание 6 — планиметрическая задача

Ошибки: в задачах с окружностями.

Видов этого задания очень много, но все они базируются на основных понятиях и теоремах геометрии.

Задача. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 75°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.

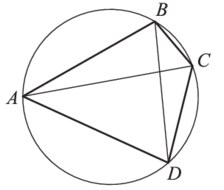
Решение. В этой задаче проверяется знание свойств вписанных углов. Вписанные углы, опирающиеся на одну и ту же дугу, равны. В нашем случае на дугу CD опираются два вписанных угла CAD и CBD. Значит, угол

ABC = ABD + CBD = 75° + 35° = 110°.

Задание 7 — производная функции

Ошибки: спутать график самой функции и её производной; забыть учесть отрезок, на котором нужно искать ответ.

В этом задании проверяется наличие базовых знаний о производной: точки экстремума (минимума и максимума), а также геометрический и физический смысл производной.

Рассмотрим два примера.

Задача 1. На рисунке изображён график функции y = f(x), определённой на интервале (-6; 8). Определите количество целых точек, в которых производная функции f(x) положительна.

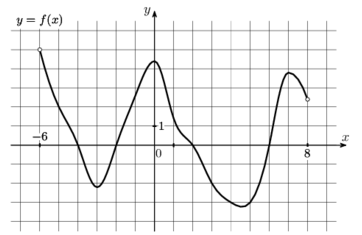
Решение. Нам даётся график самой функции y = f(x). Производная положительна там, где функция возрастает. Целые точки, лежащие на участках возрастания, это -2, -1, 5, 6. Значит, правильный ответ 4.

В следующей задаче уже даётся график производной, а также указан отрезок, на котором требуется найти количество точек максимума.

Задача 2. На рисунке изображен график y = f′(x) — производной функции f(x), определённой на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6; 9].

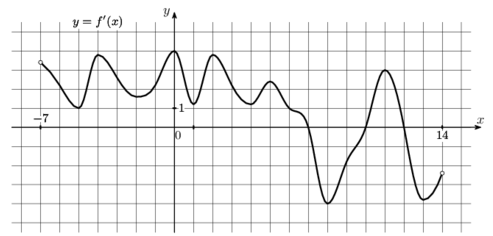
Решение. Точка максимума — это такая точка, в которой производная равна нулю либо не существует и при переходе через неё меняет знак с + на -.

В нашем случае на отрезке [-6; 9] находится единственная точка максимума x = 7. Обратите внимание: ответом является число 1, так как требуется указать количество точек максимума.

Будьте внимательны — в этой задаче можно совершить целых три ошибки:

• спутать функцию и её производную;
• не учесть заданный отрезок;
• указать саму точку, а не их количество.

Задание 8 — стереометрическая задача

Ошибки: невнимательное чтение условий, арифметические ошибки.

Задача 1. Найти площадь поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.

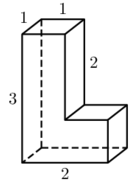
Решение. В задаче требуется найти площадь поверхности многоранника. Имеем

S = (1 · 3) · 2 + (2 · 1) · 2 + (1 · 3) · 2 + (1 · 1) · 2 = 6 + 4 + 6 + 2 = 18.

А вот следующая задача.

Задача 2. Найти объём многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.

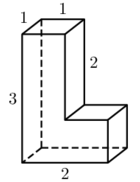
Решение. Искомый объём найдём как сумму объёмов прямоугольного параллелепипеда со сторонами 1, 1, 3 и куба со стороной 1. Имеем

V = 1 · 1 · 3 + 1 · 1 · 1 = 4.

Задание 9 — вычисления и преобразования

Ошибки: в тригонометрических задачах.

Здесь требуется найти значение некоторого математического выражения, как правило, показательного, логарифмического, алгебраического или тригонометрического. С последним типом выражений школьники обычно справляются хуже всего. Необходимо обязательно знать основные тригонометрические тождества, формулы приведения, табличные значения и знаки тригонометрических функций по четвертям.

Задача. Найдите значение выражения

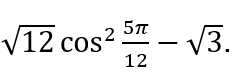
Решение. Применим формулу для косинуса двойного угла, а также формулы приведения, получим:

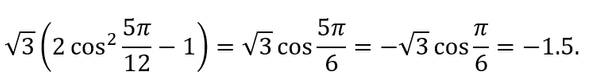
Задание 10 — применение математических знаний в повседневной жизни

Ошибки: арифметические.

Как правило, от ученика требуется подставить все указанные в задаче значения в формулу и решить уравнение или неравенство.

Задача. Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб. за ед.) задаётся формулой q = 100 — 10p. Выручка предприятия r (в тыс. руб. за месяц) вычисляется по формуле r(p) = q · p. Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 240 тысяч рублей. Ответ дайте в тысячах рублей за единицу.

Решение. Составим выражение для выручки r(p) = (100 — 10p) · p.

Решив неравенство (100 — 10p) · p ≥ 240, находим p ∈ [4; 6].

Таким образом, наибольшее значение цены равно 6.

Задание 11 — текстовые задачи

Ошибки: арифметические просчёты, неправильно составленное уравнение, невнимательное чтение условий задачи.

Здесь могут встретиться задачи на движение, работу, концентрацию, проценты и арифметическую прогрессию.

Задача. Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 километров тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.

Решение. Начнём с перевода единиц измерения: 750 м/мин = 45 км/ч. Пусть скорость товарного поезда равна x км/ч. Тогда скорость скорого поезда равна (x+45) км/ч. Так как на путь длиной 180 километров товарный поезд тратит на 2 часа больше, то имеем уравнение: 180/x = 180/(x+45) + 2.

Решив уравнение, находим x = 45.

Мы не рассматриваем отрицательный корень нашего уравнения x = -90, поскольку скорость в таких задачах считается положительной величиной.

Задание 12 — производная функции

Ошибки: неправильное вычисление производной сложной функции, производной произведения и частного; невнимательное чтение условий.

Часто ученики путают точку минимума/максимума и минимальное/максимальное значение функции. Рассмотрим задачи.

Задача 1. Найдите наименьшее значение функции

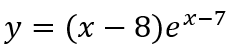
на отрезке [6; 8].

Решение. В задаче нужно найти наименьшее значение. Для этого следует вспомнить алгоритм нахождения наибольшего и наименьшего значения функции на отрезке.

В результате наименьшее значение функции равно -1, достигается в точке минимума x = 7.

Задача 2. Найдите точку минимума функции

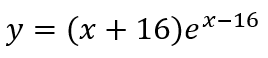
Решение. Для нахождения точек экстремума (минимума и максимума) применяем следующий алгоритм:

В нашем примере производная равна нулю при x = -17 и меняет знак при переходе через эту точку с минуса на плюс. Значит, x = -17 — искомая точка минимума.

Также нельзя забывать о случаях, когда производная всегда положительна либо отрицательна.

Задача 3. Найдите наименьшее значение функции

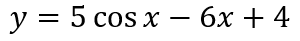
на отрезке [-3π/2; 0].

Решение. Производная такой функции всегда отрицательна, а значит, функция убывает. Убывающая функция принимает своё наименьшее значение на отрезке на правом конце, а значит, правильный ответ y(0) = 9.

Хочется пожелать успеха всем школьникам, сдающим ЕГЭ в этом году. До экзамена осталось достаточно времени, чтобы пройтись по всем прототипам заданий с кратким ответом. При подготовке советую использовать портал «Решу ЕГЭ», а также обновлённую версию открытого банка заданий — она стала намного удобнее.