Как решать олимпиадные задачи по математике, не зная сложных формул

Чтобы хорошо решать математические задачи, нужно хорошо знать математику, и только? На самом деле всё не так однозначно. Математика — это не только умение хорошо считать, даже если речь о младших классах, но ещё и способность рассуждать логически, умение мыслить абстрактно и множество других навыков.

Создатели международной математической онлайн-олимпиады BRICSMATH.COM для учащихся 1–11-х классов, которая проходит на платформе «Учи.ру» до 13 декабря, готовы на конкретных примерах доказать, что математика — это всегда нечто большее. Попробуем решить несколько олимпиадных задач вместе с Сергеем Шашковым, специалистом «Учи.ру»?

Задача № 1. Переливалки

Есть задача на переливание, которая популярна в соцсетях. Условие звучит так: есть два ведра ёмкостью 3 литра и 5 литров и неограниченный запас воды. Как точно отмерить 4 литра?

В олимпиадной версии популярная задача переосмыслена. Сюжет немного другой: ёмкостей много, воду из них выливать нельзя, и нужно сделать так, чтобы во всех сосудах количество воды стало одинаковым.

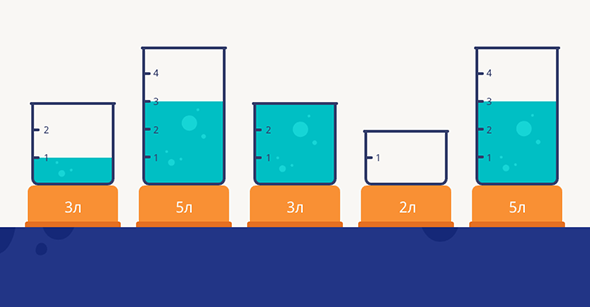
Начнём с того, что посчитаем суммарный объём воды во всех сосудах. Он не меняется и всё время составляет 1 + 3 + 3 + 3 = 10 л. Чтобы воды во всех сосудах было поровну, 10 литров нужно будет разделить на пять частей: получится по 2 литра в каждом сосуде. Значит, двухлитровый сосуд можно использовать как мерную ёмкость: можно по очереди опустошать очередной сосуд, затем наполнять двухлитровую ёмкость и переливать жидкость из неё в готовый пустой сосуд.

Решать задачу

Задача № 2. Мария-путешественница

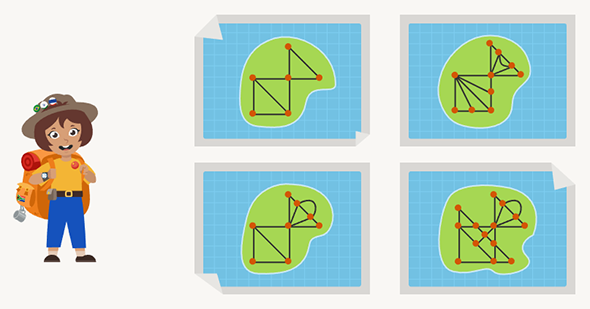
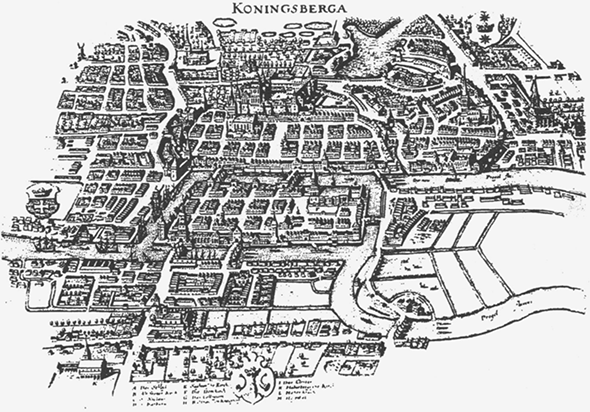
Эта детская олимпиадная задачка создана по мотивам известной задачи о семи кёнигсбергских мостах — старинной математической задачи о том, можно ли пройти по всем семи мостам Кёнигсберга, не проходя ни по одному из них дважды. Впервые она была решена в 1736 году математиком Леонардом Эйлером, который доказал, что так пройти по мостам нельзя. С тех пор пути, проходящие по всем мостам ровно по одному разу, называются эйлеровыми. А замкнутые пути — эйлеровыми циклами.

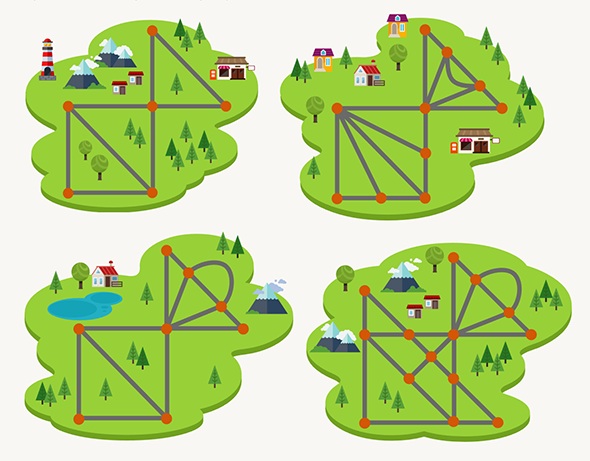
Вернёмся к Марии-путешественнице. Предположим, что она может прилететь в некоторую точку, после чего ей нужно будет обойти все дороги ровно по одному разу. Тогда входы-выходы из точек будут выглядеть так: вышла из первой точки, вошла-вышла, вошла-вышла, ещё несколько раз вошла-вышла, вошла и — ура, победа! Во всех точках, кроме первой и последней, вход и выход всегда идут парой. Значит, в каждой точке, кроме старта и финиша, дороги должны разбиваться на пары. Если вдруг они не разбиваются хотя бы в трёх точках, то нужного пути найти не удастся. Это видно на примере ниже:

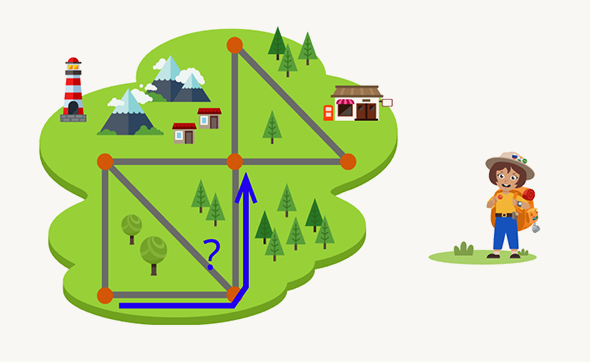
Допустим, что точек, в которых дороги не бьются на пары, всего две. Тогда нужно начинать путь из любой их них — путь всегда завершится во второй точке. Ещё может оказаться, что дороги бьются на пары в каждой точке. Этот случай оставим читателям, он приятно удивит.

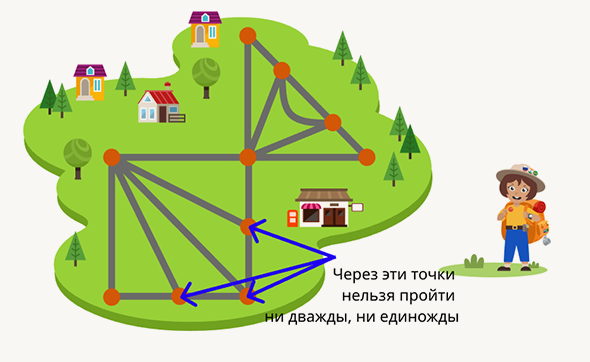
Кстати, математики называют подобные картинки графами, точки — вершинами, дороги — рёбрами. Число дорог, сходящихся в точке, называют степенью вершины. Но чтобы решить задачу про Машу-путешественницу, ребёнку не обязательно это знать: достаточно проявить смекалку и логику.

Решать задачу

Задача № 3. Участок

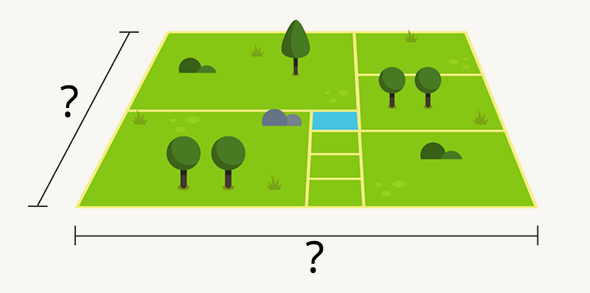
Эта задача для многих может показаться сложной. Кого-то пугает перспектива, а кто-то просто забывает, что у квадратов все стороны равны. Для решения достаточно знать это базовое правило и применить смекалку.

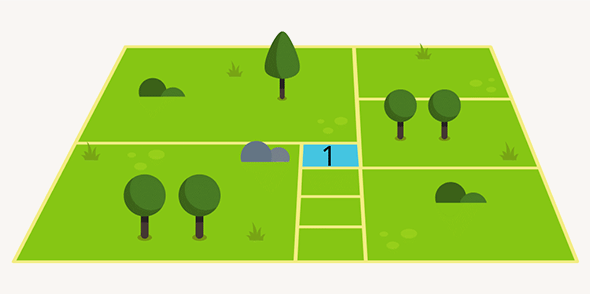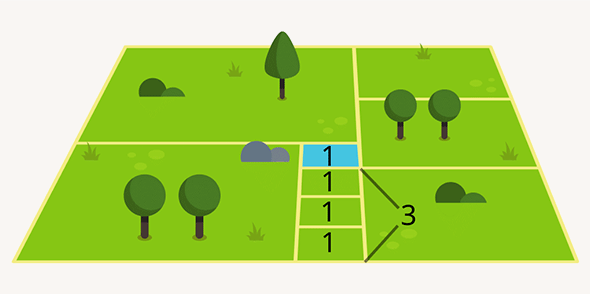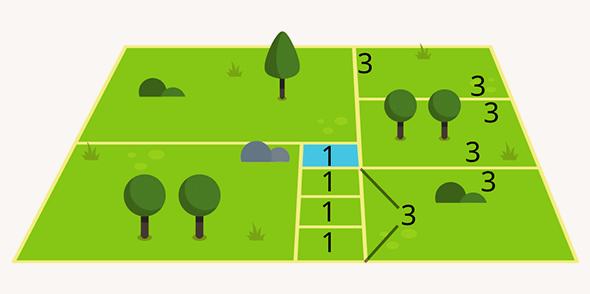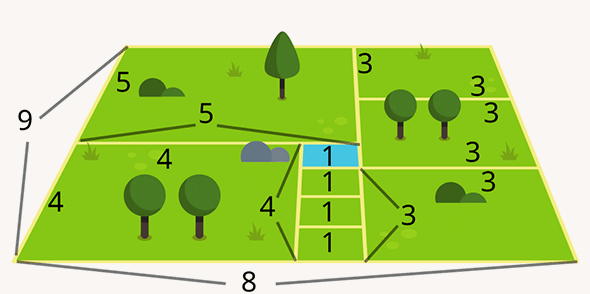
Если предположить, что размер пруда 1 × 1, то размеры каждого квадратика с общей с прудом стороной — тоже 1 × 1. Дальше эти квадраты можно использовать как линейку. Например, сразу получить размер левого нижнего квадрата — 4 × 4, или правого нижнего — 3 × 3. Так, двигаясь от соседа к соседу, можно получить стороны всех квадратов и решить задачу.

Решать задачу