Арифметика в Третьяковке
В Москве, в Государственной Третьяковской галерее, есть замечательная картина «Устный счёт» известного художника Николая Петровича Богданова-Бельского (мы рассказывали о нём в этом номере журнала).

Написана эта картина в 1895 году, а запечатлён на ней знаменитый народный учитель, популяризатор науки, профессор Московского университета Сергей Александрович Рачинский со своими учениками. В 70-х годах XIX века Рачинский неожиданно бросил карьеру, жильё в Москве и приличное профессорское жалование — и уехал в село Татево в Тверской области, где до самой смерти преподавал крестьянским детям математику и другие предметы в народной школе. Художник Богданов-Бельский, кстати, был одним из учеников Сергея Александровича.
Внимательно рассмотрев интерьер школы, костюмы учителя и детей, обратим внимание на доску. На доске написана следующая арифметическая задача:
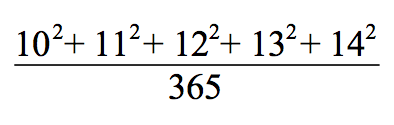
Попробуйте в наш прогрессивный, продвинутый и высокотехнологичный XXI век сделать то же самое, что делали крестьянские дети 10-12 лет в конце позапрошлого века — то есть решить эту задачу «в уме», не заглядывая в Интернет, не включая калькулятор и не используя бумаги и карандаша. Интересно, что у вас получится?
Решить эту задачу можно несколькими способами. Можно через таблицу квадратов, можно через формулу квадрата суммы. Нам нравится красивое решение через арифметическую прогрессию: известно, что квадраты чисел 10, 11, 12, 13 и 14 отличаются друг от друга на числа, образующие прогрессию с разностью 2 — то есть 21, 23, 25 и 27. Поэтому:
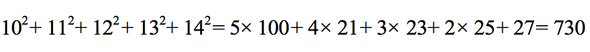
Ну а дальше делим 730 на 365 и получаем в ответе 2. Однако самое простое решение — через так называемые «последовательности Рачинского». Это красивое арифметическое открытие Сергей Александрович совершил самостоятельно и широко использовал для составления таких вот хитрых задач. Оказывается, что:
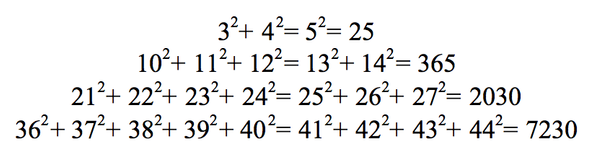
И так далее. В частности, сумма во второй строке равна 365. Тогда в задаче на картине на доске сверху в дроби, по сути, записано 365 + 365, а делим мы это всё на 365 — то есть в ответе получаем 2 (не оценку «2», а число 2) буквально за считанные секунды!

Что такое архетип, интеграл, аналемма, параллакс и теория хаоса? Почему наша галактика плоская? Можно ли измерить добро и зло? Рассказывает журнал «Лучик». Полистать номера журнала можно здесь.








